Mesterséges intelligencia - 9. előadás
Valószínűségi hálók

Letöltés PDF-ként

Bayes szabály nehézségei

• priori feltételes és együttes valószínűségek begyűjtése nehéz és költséges
• ember rossz valószínűségbecslő
• Bayes-szabály sok számítást igényel

Valószínűségi hálók

• más néven Bayes-háló → egy gráf

  • csomópontok → valószínűségi változók egy halmaza
  • csomópontok között → irányított élek halmaza (Y → X = Y-nak közvetlen befolyása van az X-re)
  • minden csomópont → feltételes valószínűségi tábla → P(X | Szülők(X))
  • a gráf nem tartalmaz irányított kört → DAG
  • valószínűségi változó = egy állítás a problémáról

• feltételes valószínűségi tábla - FVT

  • egyes csomóponti értékek feltételes valószínűsége, az adott sorhoz tartozó szülő feltétel esetén

  • ahol egy szülői feltétel → szülői csomópontok értékeinek egy lehetséges kombinációja

  • pl Betörés → Riasztás és Földrengés → Riasztás, akkor

    B	F	P(R) = P(R|B ∧ F)
    i	i	0.95
    i	h	0.95
    h	i	0.28
    h	h	0.001

  • Így → kevesebb dolgot kell számolni, mint ha az összes együttes valószínűséget néznénk (2ⁿ-1)

    • HA minden mindennel összefügg → akkor ez sem segít :(

• Bayes-hálók → White box modell (belső működése is értelmezhető)

  • a Neurális hálók pl általában nem ilyenek, hanem black box modellek

• együttes valószínűségi eloszlás dekomponált leírása

  • 

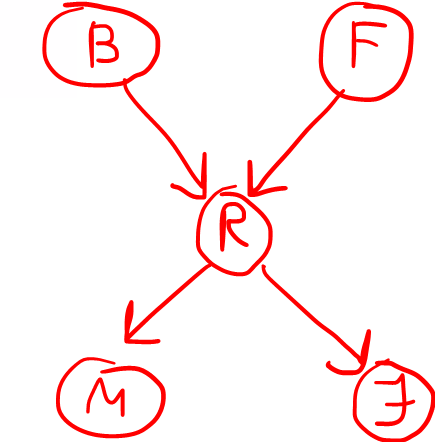
  • P(J M R ¬B ¬F) = = P(J | M R ¬B ¬F) * P(M R ¬B ¬F) =

    = P(J | R) * P(M | R ¬B ¬F) * P(R ¬B ¬F) = = P(J | R) * P(M | R) * P(R | ¬B ¬F) * P(¬B) * P(¬F)

• amit tudunk:

  1. minden csomópont feltételesen független a nem leszármazottaitól, ha a szülői adottak
  2. minden csomópont feltételesen független minden mástól, ha a markov-takarója adott
     • markov-takaró: a szülei, a gyerekei, és a gyerekeinek a szülei.
     • ez elszigeteli a modell többi részétől!

• háló építésének lépései:

  1. határozzuk meg a problémát leíró változókat
  2. határozzunk meg egy sorrendet
  3. amíg marad érintett változó
     1. válasszuk a következő X_i-t, adjuk a hálóhoz
     2. legyenek X_i szülei a már gráfba levő csomópontok azon minimális halmaza, amiktől feltételes függetlenségben áll
     3. definiáljuk X_i feltételes valószínűségi tábláját

• pozitívum az együttes valószínűségi eloszlásfüggvényekhez képest

  • tömörebb, lokálisan strukturált (egy komponens csak korlátos másikkal van kapcsolatban)
  • inkább lineáris komplexitás növekedés (mint exponenciális)

Naív Bayes-hálók

• egy szülőhöz tartozik több gyermek csomópont