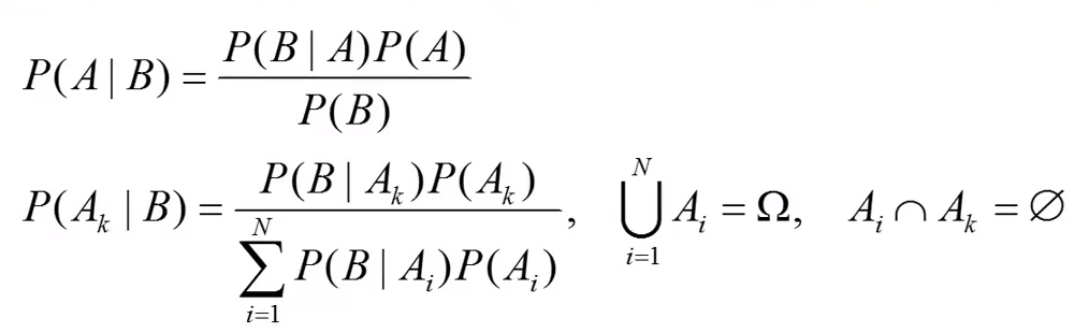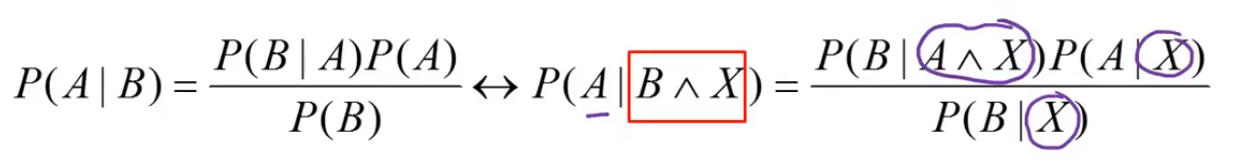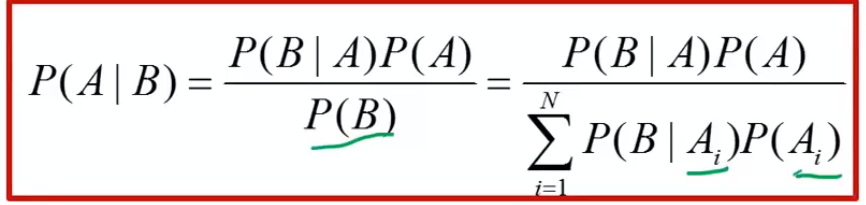Mesterséges intelligencia - 7. előadás
Bizonytalanság kezelése

Letöltés PDF-ként

Bizonytalan tudás

Bizonytalan tudás lehetséges okai

• "lazaság, lustaság": a részletes kapcsolatok megfogalmazása túl nehéz, a használatuk szintén nehézkes
• elméleti ismeretek hiánya: adott problématerület elméleti feltárása még nem zárult le, vagy sose lehet lezárni
• gyakorlati ismeretek hiánya: nem minden, a szabályokban hivatkozott feltétel ismert a szabályok alkalmazásakor

Valószínűségi axiómák

• 0 ≤ P(A) ≤ 1
• P(Igaz) = 1, P(Hamis) = 0
• P(A ∨ B) = P(A) + P(B) - P(A ∧ B)
• P(¬A) = 1 - P(A)
• P(A) = P(A ∧ B) + P(A ∧ ¬B)

Valószínűségi állítások

• bináris → P(Lyuk = Igaz)
• többértékű → P(Időjárás = Esős)
• folytonos → P(Hőmérséklet < 22 °C)

Pár szabály, átalakítás

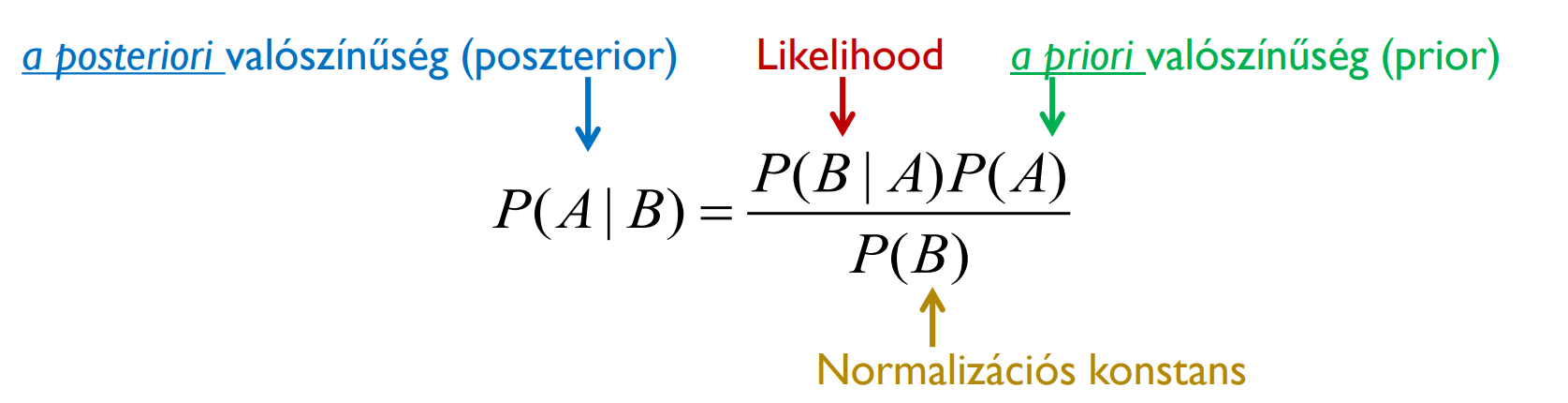
• Feltételes valószínűség → P(A | B) = P(A B) / P(B)
• Lánc szabály → együttes valószínűség felírható feltételes valószínűségek szorzataként
• Bayes-tétel
  • 
  • miért fontos?
    • sokszor rendelkezünk kauzális (ok-okozati) tudással
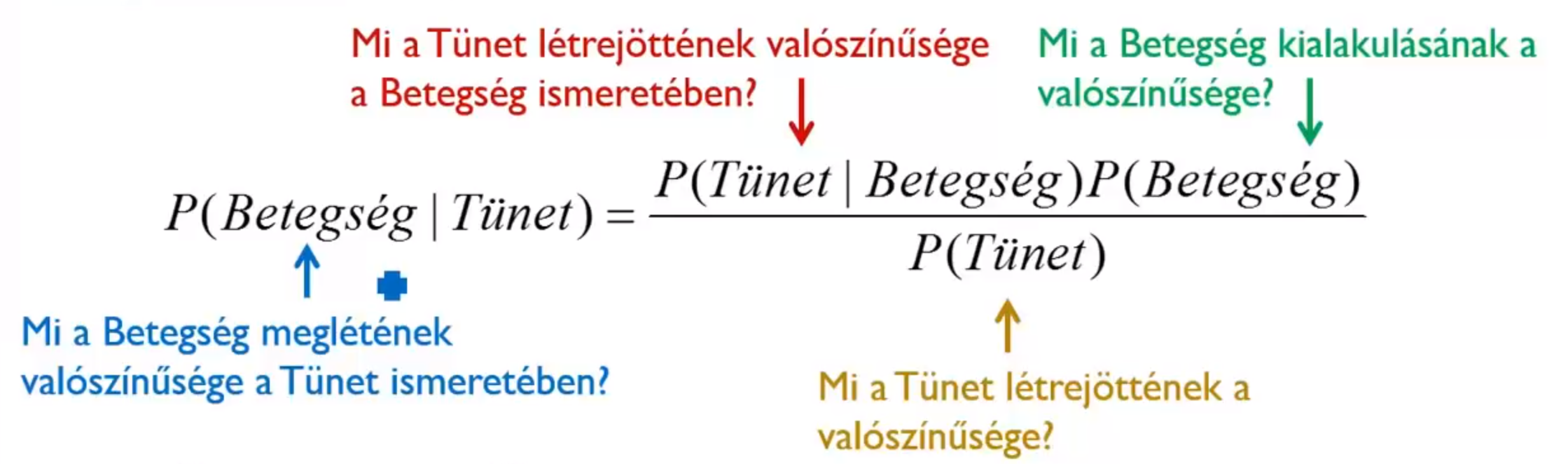
    • pl1: mi az adott tünet valószínűsége egy adott betegség függvényében
    • pl2: mi a valószínűsége a riasztásnak tűz esetén (adott riasztónál pl)
  • sokszor kell az evidencia (következmény) felől az ok-ra következtetni
    • pl1: tünetet látom, lehetett e adott betegség a kiváltó ok
    • pl2: riasztás van, lehetett e tűzeset miatt
  • okság irány: könnyebb, betegségről tünetre következtetni
  • diagnosztikai irány: nehezebb, tünetről betegségre következtetni
  • 
  • 
  • Bayes-tétel műveletek:
    • 
    • 

Valószínűség értelmezése

• frekventista nézőpont: a valószínűség objektív, események gyakoriságából számítható
  • valószínűség (frekventista definíciója): A esemény valószínűsége az a számérték, amely körül az esemény relatív gyakorisága (f_A) ingadozik, ha egyre több kísérletet végzünk
  • P(A) = lim _n→∞ f_A
• bayesi nézőpont: a valószínűség egy eseménybe vetett hiedelem mértéke
  • valószínűség (bayesi definíciója): A esemény valószínűsége az adott esemény bekövetkezési esélye
  • a jelenlegi helyzettől megkülönböztethetetlen esetek mekkora hányadában fog bekövetkezni az adott esemény
  • Priori valószínűségekből indulunk ki, új evidencia érkezésekor azokat frissítjük

Együttes valószínűség-eloszlás

• P(X₁, ..., X_n) → minden egyes elemi eseményhez valószínűséget rendel
• táblázat → cellája az adott állapot valószínűsége, pl P(időjárás, hőmérséklet) → bazinagy táblázat lesz
  • elemi események, mert nem lehet egyszerre felhős-meleg és napos-hideg
  • táblázat elemeinek összege 1
• marginális elosztások → egy változóra nézett vetület → adott értékbek tartozó sorban/oszlopban levő értékek összege
• pozitívum: együttes eloszlás birtokában → mindenre választ kapunk
• negatívum: nem megy 10-nél több változóra → P(X₁, ..., X_n) esetén → 2ⁿ-1 független valószínűségérték
  • egy diagnózishoz → exponenciális számú valószínűség kellene :(
  • ha 1 is megváltozik, akkor csomót újra kell számolni! :(

Bayesi frissítés

• egyesével gyűjtjük a tényeket, majd módosítjuk az ismeretlen változóval kapcsolatos korábbi hiedelmi mértéket
• TODO itt hirtelen vége a felvételnek :O