Kihagyás

Mesterséges intelligencia - 6. előadás
Logikai ágens, elsőrendű logika

Letöltés PDF-ként

Rezolúció

  • Egy Q-ról akarjuk eldönteni, hogy igaz e vagy hamis.
  • lépései:
    • TB átírása klóz formába
    • Q kérdés negálása, negált Q kérdés átírása klóz formára
    • kiterjesztés TB' = TB ∪ ¬Q
    • rezolúciós lépés ciklikus elvégzése → üres rezolvenst kapunk
    • tehát TB' egy ellentmondást tartalmaz, és mivel TB igaz volt biztosan ¬Q miatt romlott el, azaz Q igaz kell, hogy legyen!
  • klóz formára hozás
    1. ekvivalencia elhagyása: A ⇔ B = (A → B) ∧ (B → A)
    2. implikáció elhagyása: A → B = ¬A ∨ B
    3. negálás atomi formulák szintjére (de Morgan): ¬(A ∨ B) = ¬A ∧ ¬B
    4. diszjunkciók literálok szintjére (disztributivitás): (A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C)
    5. konjunkciók elhagyása (diszjunktív klózokra bontás): csak ¬ és ∨ maradhat, azaz az és-ek helyett külön mondattá szedjük őket
  • probléma: túl sok ítéletszimbólumot kell kezelni, nehézkes a változások kezelése → lassú a következtetési eljárás
    • ahol jó: formális modell-ell, MI tervkészítés, auto tesztminta-generálás, szoftver-verifikáció, stb

Elsőrendű logika

  • objektumok: más obj-tól megkülönböztethető identitású, tulajdonságokkal rendelkező dolog
  • relációk: kapcsolatok, lehet n-elemű vagy egyelemű (ezek a tulajdonságok)
  • függvény jellegű relációk: egy érték egy adott bemenetre (pl: apja, egyel több mint)
  • szintaktika és szemantika
    • konstans szimbólumok: X, János, K21
    • predikátum szimbólumok: kerek(X), bátyja(József, Anna)
    • függvény szimbólumok: János = apja(Béla), apja(János, Béla) = Igaz
  • építőelemek:
    • term: egy objektumre vonatkozó kifejezés (János, bal-lába(apja(János)), ...)
    • atom: bátyja(Géza, Árpád)
    • atomi mondat: predikátum szimbólum és az argumentumait jelentő termek tényeket fejez ki (igazságértéke van)
    • összetett mondat: bátyja(Misi, János) → házas(apja(Misi), anyja(János))
    • kvantorok:
      • univerzális kvantor: ∀ (∀x. macska(x) → emlés(x))
      • egzisztenciális kvantor: ∃ (∃x. magyka(x) ∧ úszik(x))
    • egyenlősség: (term1 = term2) adott implementáció mellett és akkor és csak akkor, ha term1 és term2 ugyanarra az objektumra vonatkozik
    • ∀ és ∃ kapcsolata:
      • ∀x ¬szeret(x, Répa) = ¬∃x szeret(x, Répa)
      • ∀x szeret(x, Fagylalt) = ¬∃x ¬szeret(x, Fagylalt)
    • fontos: mivel mi adjuk a konstansok, predikátumok és függvényszimbólumok neveit → fontos, hogy ha kettő kettő ugyan azt jelenti, azt logikailag is leírjuk! (ne csak mi tudjuk, hogy a nagytestű és dögnagy ugyanaz!)

Modell alapú következtetés?

  • probléma:

    • összes modell felsorolása nagyon sok, DE megszámlálható
    • függvények egymásba ágyazhatók végtelen mélységben! (apja-fia végtelen ismétlése)
      • megoldás1: redukció ítéletlogikai következtetésre
      • megoldás2: következtetési lépések kiterjesztése

  • redukció ítéletlogikai következtetésre → grounding

    • változó nélküli term → alapterm (grounding)
    • változó nélküli predikátum kalkulus → ítélet kalkulus
    • új TB = minden univerzális mondat minden lehetséges példányosítása
      • egy alapmondat vonzata az új TB-nek, ha vonzata volt az eredeti TB-nek is
      • függvény = végtelen sok alapterm → határt kell húzni nekik
    • teljes: minden igaz állítás belátható
    • vonzat csak félig eldönthető: állítás hamis volta nem mutatható ki
      • bizonyítási eljárásnak igaz állítás esetén van kilépési pontja
      • hamis állítás esetén nincs, közben nem dönthető el
      • AZAZ gépen véges erőforrások miatt elvben nem mutatható ki egy állításhalmaz konzisztenciája

  • következtetési lépések kiterjesztése

    • unizerzális kvantor eliminálása

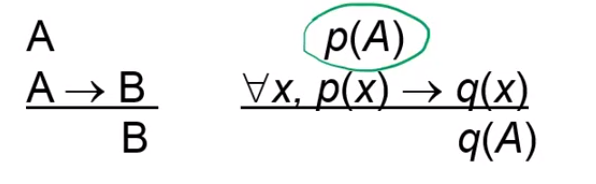
      • image-20201025114116986
      • illesztés = unifikálás (mit mivel ) + behelyettesítés (konkrét érték)

    • egzisztenciális kvantor elminimálása → skolemizálás

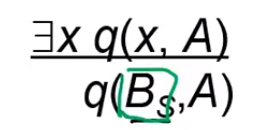
      • image-20201025114601535

      • BS = Skolem konstans, a feladatban önálló léttel NEM rendelkező objektum

        • lehet függvény is! (ami minden x-hez egy külön skolem konstanst rendel hozzá)

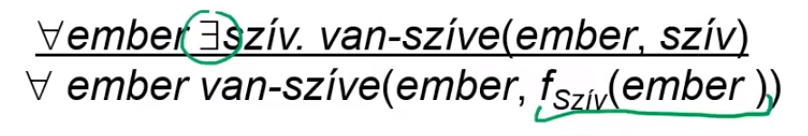
      • image-20201025114620929

        • szükség van az fSZÍV Skolem függvényre, ami megadja az adott ember szívét

      • egyesítés megy, ha:

        x y eredmény
        változó-1 változó-2 ✔
        változó konstans ✔
        konstans változó ✔
        konstans-1 konstans-2 ✖
        változó f(változó) ✖

  • gépi bizonyítás

    • Modus Ponens alapú biz. → NEM teljes
    • elsőrendű logikai biz. → teljes
    • algoritmizált "hogyan" → rezolúció → DE a félig eldönthetőség megmarad
    • transzformáció klóz formára
      1. ekvivalencia elhagyása: A ⇔ B = (A → B) ∧ (B → A)
      2. implikáció elhagyása: A → B = ¬A ∨ B
      3. negálás atomi formulák szintjére (de Morgan): ¬(A ∨ B) = ¬A ∧ ¬B, ¬∀x p(x) = ∃x ¬p(x)
      4. Egzisztenciális kvantorokat eltüntetni: Skolemizálás
      5. Ha szükséges, a változókat átnevezni: ∀x p(x) ∨ ∀x q(x) helyett ∀x p(x) ∨ ∀y q(y)
      6. Univerzális kvantorokat balra kihejezni: ...∀x...∀y... = ∀x∀y...x...y
      7. diszjunkciók literálok szintjére (disztributivitás): (A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C)
      8. konjunkciók elhagyása (diszjunktív klózokra bontás): csak ¬ és ∨ maradhat, plusz a kvantorok
      9. ha szükséges, a változókat átnevezni
      10. univerzális kvantorokat elhagyni → csak ¬ és ∨ maradhat, azaz az és-ek helyett külön mondattá szedjük őket
    • Rezolúció bizonyítás procedúrája → adott állítás halmaza F, a bizonyítandó állítás Q
      1. Az F halmaz összes állítását konvertáljuk klóz formába → F'
      2. Negáljuk a Q-t, és konvertáljuk klóz formába, adjuk hozzá F'-hez
      3. Ismételjük a ciklust (3-4-5 pont):
        1. ellentmondásra rá nem futunk
        2. előrehaladást nem tapasztaljuk
        3. az erőforrások előre meghatározott mennyiségét ki nem használjuk
      4. Válasszunk meg két klózt és alkalmazzunk rezolúciós lépést
      5. Ha a rezolvens üres, megvan az ellentmondás. Ha nem, adjuk hozzá a többi klózhoz és folytatjuk a 3. pontot.
    • Rezolúciós stratégiák = klózok kiválasztási heurisztikái
      1. Egység rezolúció → Horn-klóz alakú TB-ban az eljárás teljes, különben nem!
      2. Set of Support:
      3. MI A LÓFASZ EZ A 31. DIA? KONKRÉTAN EGY SZÓT NEM MOND EL BELŐLE ÉRTELMESEN... 1:01:00 előtt FUCKING TODO
    • logikai prorgamozás - Prolog
      • nem teljes → időkorlát van!

  • Ontológia

    • cél: a tudás megosztása (érthetően). Adott tárgyterület részletes leírását valósítja meg.
    • összetevők: fogalmak (osztály), tulajdonságok és relációk a fogalmak közt (taxonómia (isA, partOf), reláció, attribútum, szerep)
    • tárgyterület részletes leírása:
      • megkötések → típus megkötés, számosság (1 alatti), értéktartomány (0 és 50 közti), X nagyobb mint Y, X és Y különböző
      • konkrét érték megadása
    • ontológiák típusai
      • szemantika szerinti csoportosítás
        • taxonomy - relációs modell szerinti
        • thesaurus - ER
        • conceptual model - RDF/S, XTM, UML
        • logical theory - OWL, ...
        • Elsőrendű logika
    • Ontológia vs Relációs séma
      • ontológia → formálisan definiált kapcsolatok az entitáok közt, ember és gép is érti
      • relációs séma → implicit kapcsolatok az entitások között, interpretáció szűkséges, adatbázis szemantikájának ismerete nélkül nem használható

  • festő ágens problémája

    • amiket nem kezelünk: idő múlása, ágens cselekvéseinek leírása, környezet változása
    • idő bevezetése → szituáció kalkulus
      • idő múlása = szituációk sorozata
      • egy szituációban 1 tény igaz vagy hamis, de a következő szituációban lehet más
      • fluent = folyékony esemény
      • hatás axiómák: egy adott cselekvésnek mi lesz az eredménye
      • keret axiómák: a környezet miatt mi marad változatlan

  • TODO itt még volt valami a diasorban, de arról nem beszélt (?)