Mesterséges intelligencia - 5. előadás
Logikai ágens, szabályalapú rendszerek

Letöltés PDF-ként

Történelem

• Mycin → szakorvosi szintű első szabályalapú rendszer → tünetek alapján betegség és kezelés javaslat

Logika szerepe a komplex MI alkalmazásokban

• logikai szabályalapú következtetés és beavatkozás
  • egy vagy több feltétel logikai állításként történő megfogalmazása
  • reakciók, beavatkozások megadása logikai szabályok formájában
• IBM Watson (2011): Jeopardy kvízjáték → beszédértés, következtetés, játék

Logika

• 2 része van
  • tudás bázis: feladatspecifikus információ (elméletek + észrevételek)
  • következtető gép: feladatfüggetlen algoritmusok
• 
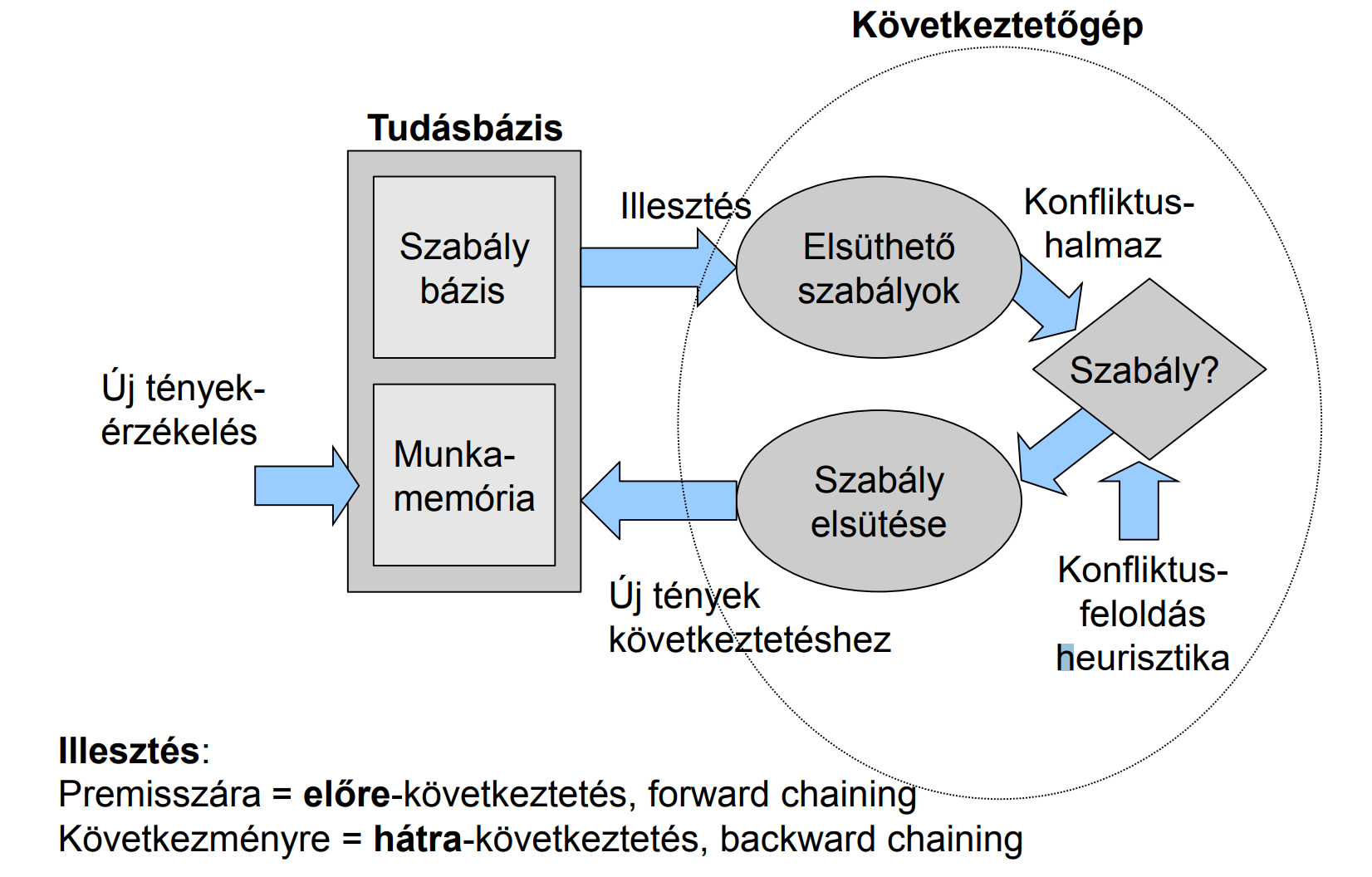
• példák ilyen rendszerekre: jogi szakértői rendszerek, ügyfélszolgálat, csetbot, stb
• előnyei:
  • látjuk a levezetést is! (hogy jutottunk pl a diagnózisig?)

Reprezentáció és manipuláció eszköze

• szintaktika: legálisan létrehozható szimbolikus mondatok

• szemantika: a világ tényei, amikre a szimbolikus mondatok vonatkoznak

• tények: valós dolgok a világban, amik egymással kapcsolatban vannak

  • vonzat: logikai konzekvencia dolgok között
  • vonzatreláció → α vonzata TB-nek: TB |= α, ha α minden olyan világban igaz, ahol TB is igaz.

• következtetés: a vonzat kiszámítása a mondatok formális manipulálásával

• bizonyítás: a következtetési algoritmus lépéssorozata

  • α bizonyítható TB-ből: TB |- α

• szintaktika és szemantika összekapcsolódása → interpretáció kell hozzá

  • az igazság függ mind a mondat interpretációjától, mind a világ aktuális állapotától

• modell

  • bármely világ, ahol a mondat igaz egy bizonyos interpretációban

  • minél több információt tudunk → annál kevesebb modellünk lesz

  • egy α mondat vonzata a TB tudásnak, ha a TB modelljei mind modelljei az α-nak is

    • ekkor ha TB igaz, akkor α is igaz, azaz
    • TB |= α, akkor és csak akkor, ha M(TB) ⊆ M(α)
    • 

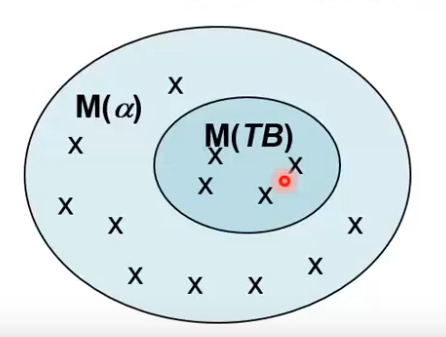
  • példa:

    

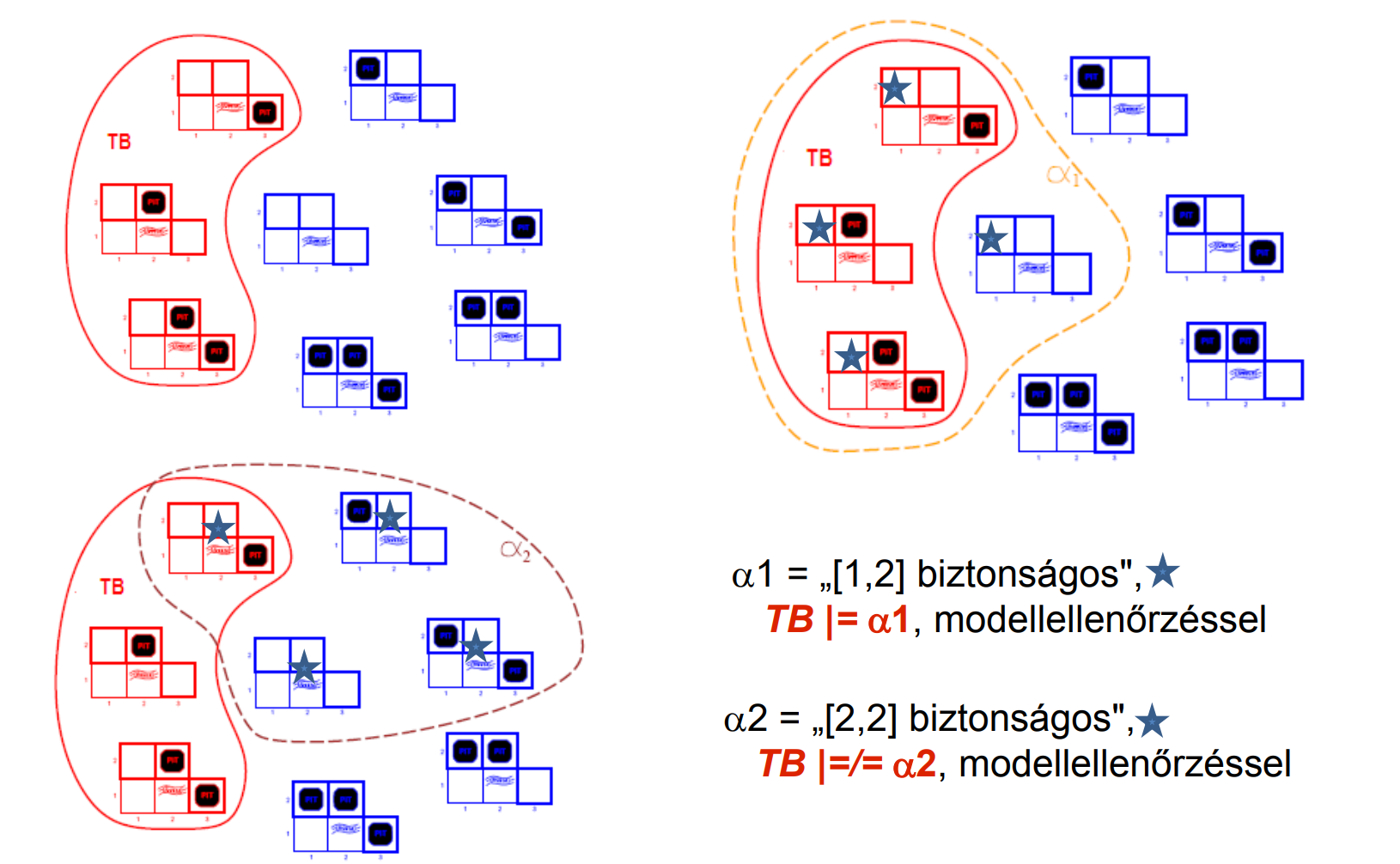
  • Ha adott egy TB, egy a következtetés

    1. létrehozhat új α mondatot, amely vonzata a TB-nak (azaz ha kikövetkeztetem, hogy [1;2] egy biztonságos mező, akkor abból létrejön egy új α mondat, ami az adott tudásbázisból következik, tehát annak vonzata)
    2. ha adott α mondat, eldöntheti hogy α vonzata-e a TB-nak (azaz ha kikövetkeztetem, hogy [1;2] egy biztonságos mező, akkor abból egy adott α mondatról eltudom dönteni, hogy vonzata-e a tudásbázisomnak)

  • igazságtartó következtetés (extenzionális), ha csak igazságfüggvényekkel dolgozik

    • (igazságfüggvény logikai értéke → csak az igazságfüggvény részeitől és logikai műveletek definíciójától függ, az interpretációtól nem!)

  • formális bizonyítás → igazságtartó következtetési eljárás lépései

  • következtetési eljárás

    • teljes: ha minden vonzatmondathoz talál egy bizonyítást (azaz ami igaz az bebizonyítható)
      • A |= B-ból A |- B
    • helyes: ha minden bizonyított mondat vonzatrelációban áll a felhasznált tényekkel (azaz ami bebizonyított, az igaz is)
      • A |- B-ból A |= B

  • érvényes (analitikus mondat, tautológia): ha minden világban minden lehetséges interpretációja igaz, függetlenül attól, hogy mit akar jelenteni és mi a világ állapota (pl van fal vagy nincs fal)

  • kiegészíthető: ha létezik olyan interpretáció, hogy valamely világban igaz. Különben kiegészíthetetlen.

• példa:

  • 
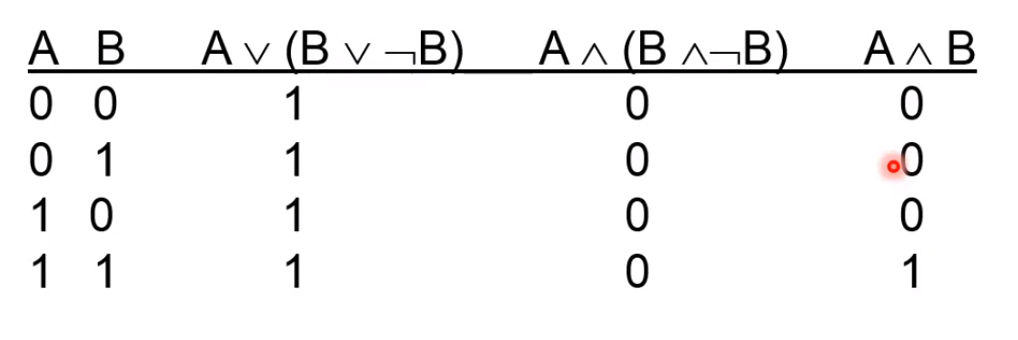
  • itt az első érvényes (minden világban 1), a második érvénytelen (B és Bnegált miatt), a harmadik kielégíthető (néhány világban teljesül, pl ahol A=1 és B=1)

• Ítéletkalkulus

  • igaz és hamis logikai konstansok, precedencia: ¬, ∧, ∨, →, ⇔
  • szemantika: minden modell i/h értéket rendel minden ítélet szimbólumhoz
  • 
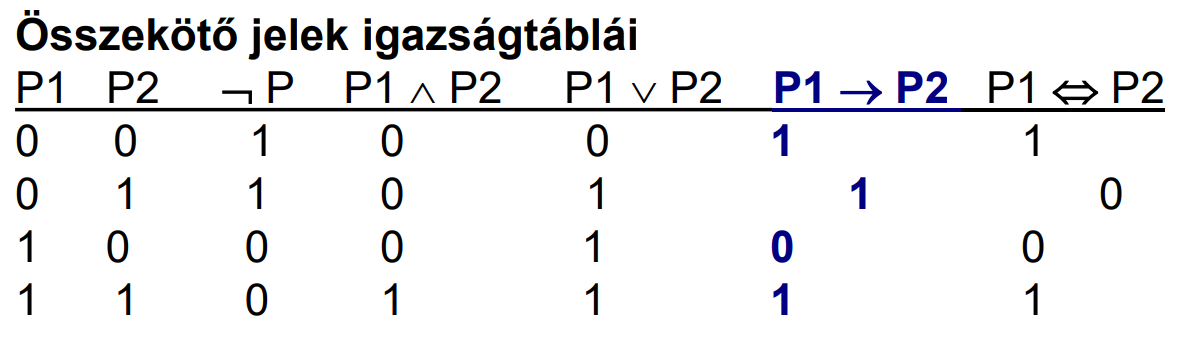
  • N argumentumon értelmezett logikai függvény 2 a 2^N-ediken → igazságtáblás kiértékelés nem nagyon lesz használható
  • 
  • Két állítás logikailag ekvivalens, ha ugyanazokban a modellekben igaz, azaz A ⇔ B akkor és csak akkor, ha A |= B és B |= A
  • TB |= α akkor és csak akkor, ha (TB → α) érvényes
  • TB |= α akkor és csak akkor, ha (TB ∧ ¬α) kielégíthetetlen

• következtetés módjai

  • modell-ellenőrzés (a mondat kielégíthető-e)
    • igazságtábla listázás
    • visszalépéses keresés
    • heurisztikus keresés modellek terében (helyes de nem teljes)
  • következtetési szabályok alkalmazása → új mondatok legális generálása régebbi mondatokból
  • bizonyításkor speciális operátorok
    • keresés általános operátorokkal (természetes dedukció)
    • teljes keresés teljes operátorral általános logikában (rezolúció, exponenciális!)
    • teljes keresés teljes operátorral redukált logikában (Horn-klózok, Modus Ponens, redukált komplexitás!)

• ítéletlogika következtetési mintái

  • modus ponens (implikáció eliminálása): A → B helyett B
  • AND eliminálása: A₁ ∧ A₂ ∧ A₃ ∧ ... helyett A₁, A₂, A₃, ...
  • AND bevezetése: A₁, A₂, A₃, ... helyett A₁ ∧ A₂ ∧ A₃ ∧ ... (TB = 1 állítás)
  • OR bevezetése: A₁, A₂, A₃, ... helyett A₁ ∨ A₂ ∨ A₃ ∨ ...
  • Dupla negálás eliminálása: ¬¬A helyett A
  • elemi rezolúció: A ∨ B helyett ha Bről tudjuk, hogy negált, akkor A biztosan ponált
  • rezolúció: Ha szerepel B ∨ A és ¬B ∨ G, akkor a kettő helyett A ∨ B használható (ha van 2 diszjunktív állításunk, és pontosan az egyik elemre igaz, hogy az egyikben ponáltan a másikban negáltan szerepel, akkor kikövetkeztethetjük, hogy a két állításban a rezolúcióban nem érintett részek maradnak csak meg)

• logikai következtetések fajtái

  • dedukció: formálisan érvényes következtetés, tudás átalakítás modellje
    • pl feltétel: ha a kutya nagy, akkor sokat eszik. tapasztalat: a kutya nagy. következtetés: sokat eszik.
  • indukció: ezek nem formálisan igazak, tömörítés, általánosítás: példákból tanulás modellje
    • pl tapasztalat: kutya1 nagy, kutya2 nagy, ..., kutya1000 nagy. induktív általánosítás: minden kutya nagy
    • formálisan NEM igaz!
  • addukció: belátás folyamata, diagnózis, magyarázatadás modellje
    • pl feltétel: ha a kutya nagy, sokat eszik. tapasztalat: a kutya sokat eszik. hipotézis: a ktuya nagy
    • formálisan NEM igaz!

• ítéletlogika eldönthető és teljes

  • beláthatóak véges algoritmussal → következtetés igazságtábla módszere teljes, DE a számítási idő exponenciális
  • egy mondathalmaz kielégíthetőségi vizsgálata NP-teljes

• ítéletlogika monoton

  • új mondat TB-hoz hozzáadásakor az eredeti TB mondatok továbbra is vonzatai maradnak az új nagyobb TB-nak
    • ha TB₁ |= a, akkor (TB₁ ∪ TB₂) |= a
  • statikus világ → akkor ez nagyon jó
  • dinamikus világ → valahogy frissíteni kell, hogy továbbra is igazak e a megszerzett tudások

• Horn klózok

  • ha ilyen formájú: P₁ ∧ P₂ ∧ P₃ ∧ ... P_n→ Q vagy ¬P₁ ∨ ¬P₂ ∨ ¬P₃ ∨ ... ¬P_n ∨ Q
  • ekkor létezik a TB méretében lineáris idejű következtetési eljárás
  • nem minden TB-beli állítás írható fel így, de ami igen → Modus Ponens-t tudunk alkalmazni
    • Modus Ponens teljes bizonyítási lépés a Horn klózok tudásbázisában

• előrecsatolt következtetés

  • minden olyan szabályt elsütünk, aminek premisszája teljesül, a következményt a TB-hez adjuk, amíg a kérdéses változó értéket nem kap

• hátracsatolt következtetés

  • kérdéses változótól visszafele lépkedünk, amíg nem találunk olyat amik igazak, és onnan mehetünk felfele.

• Wumpus következtetés

  • TODO feladta házinak a jófej bácsi :) 36. diától