Kihagyás

Mesterséges intelligencia - 4. előadás
Keresés ellenséges környezetben

Letöltés PDF-ként

Játékok típusai

  • sokféle létezik
  • tulajdonságok:
    • determinisztikus vagy sztochasztikus? (van benne véletlen?)
    • egy, kettő vagy több játékos?
    • zéró összegű játék? (egy nyertes van, ha az egyik játékos jobb helyzetbe kerül a másik rosszabba)
    • teljes információ (láthatjuk az állapotot)? (pl kártyajáték NEM ilyen)
  • algoritmus = stratégiát ad → optimális/jó választ javasol minden egyes állapotban
  • determinisztikus játékok formalizálása:
    • állapotok: S
    • játékosok: P={1..N}
    • cselekvések: A
    • állapotátmenet függvény: SxA → S
    • célállapot teszt: S → {igaz, hamis}
    • célállapot hasznosság: SxP → R
    • megoldás egy játékos számára a stratégia ami S → A
  • zéró összegű játék
    • ágensek hasznossága ellenkező, ellenséges játékosok tiszta versengéssel
  • nem zéró összegű játék
    • ágensek hasznossága független
    • kooperáció, közömbösség, versengés mind egyszerre megjelenhetnek
  • egy állapot értéke → az adott állapotból elérhető legjobb kimenetel (hasznosság)
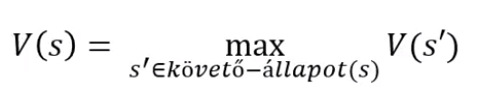
    • nem végállapotok: image-20201022165134043
    • végállapotok: V(s) = ismert

Minimax

  • ágens és ellenfele ellentétes célra törekednek

  • egyikük minimalizálni, másikuk maximalizálni akar egy adott értéket → minimax

  • minimax keresés

    • keresés állapottér gráfban

    • játékosok felváltva lépnek

    • minden csomópontra minimax érték számítása: legnagyobb elérhető hasznosság egy racionális (ügyesen játszó) ellenséggel szemben

    • végállapotok értéke kiszámítva a játék szabályaiból, és ez alapján születik döntés!

    • algoritmus:

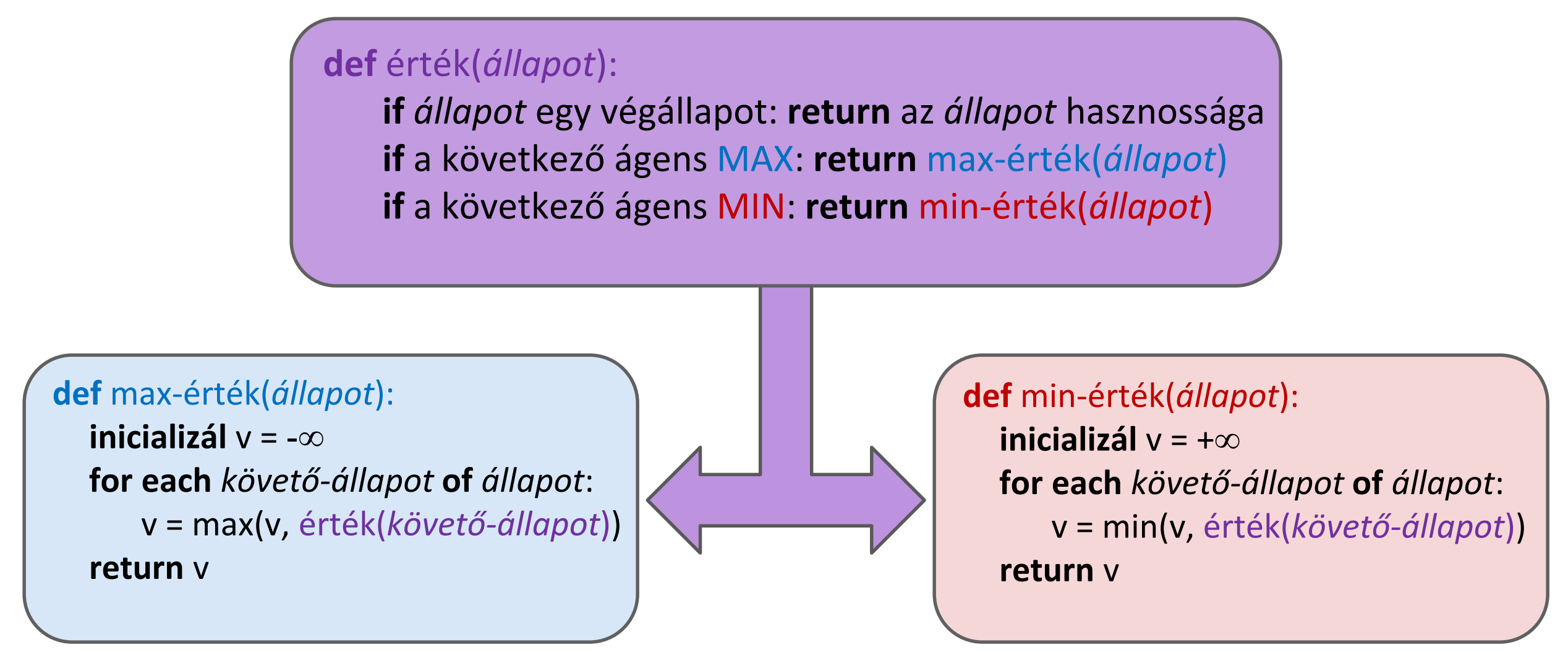
      image-20201022171910376

    • milyen hatékony?

      • gyakorlatilag egy kimerítő DFS → optimális, de nagy esetben nem lesz hozzá erőforrás
      • idő: O(bm)
      • tár: O(bm)

    • hogy lehet rajta javítani? → nyesések

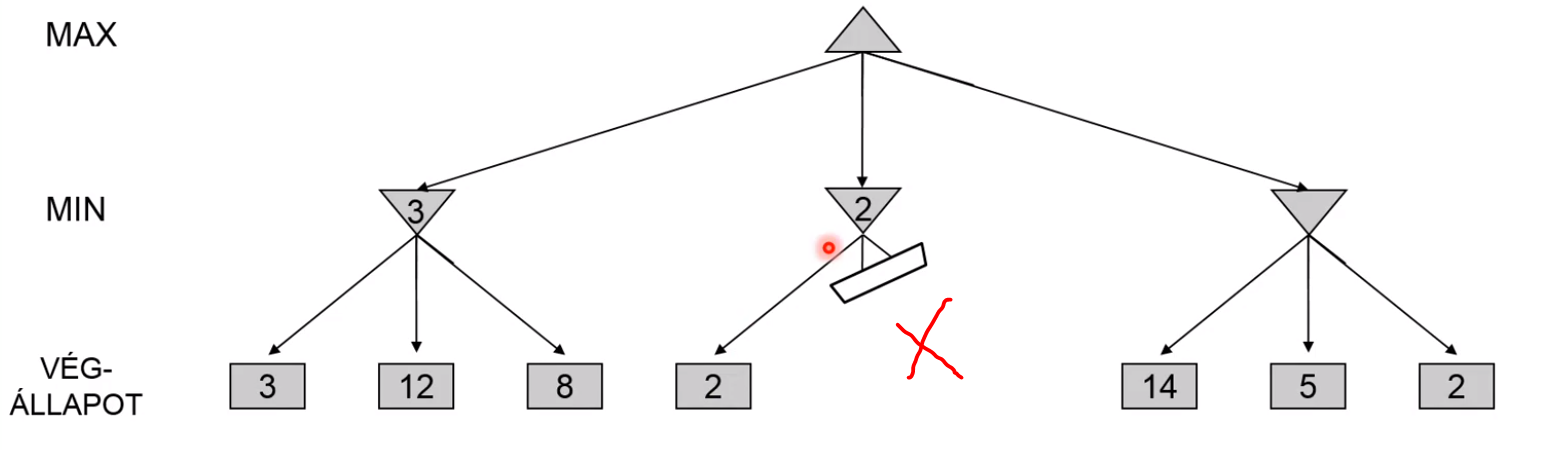
      • image-20201022170914767
      • ne fejtsük ki azt az ágat, amit biztos nem fog választani (a min ág tuti 2-t rak oda, vagy kisebbet, így a max ágnak nem fogja megérni azt választani)

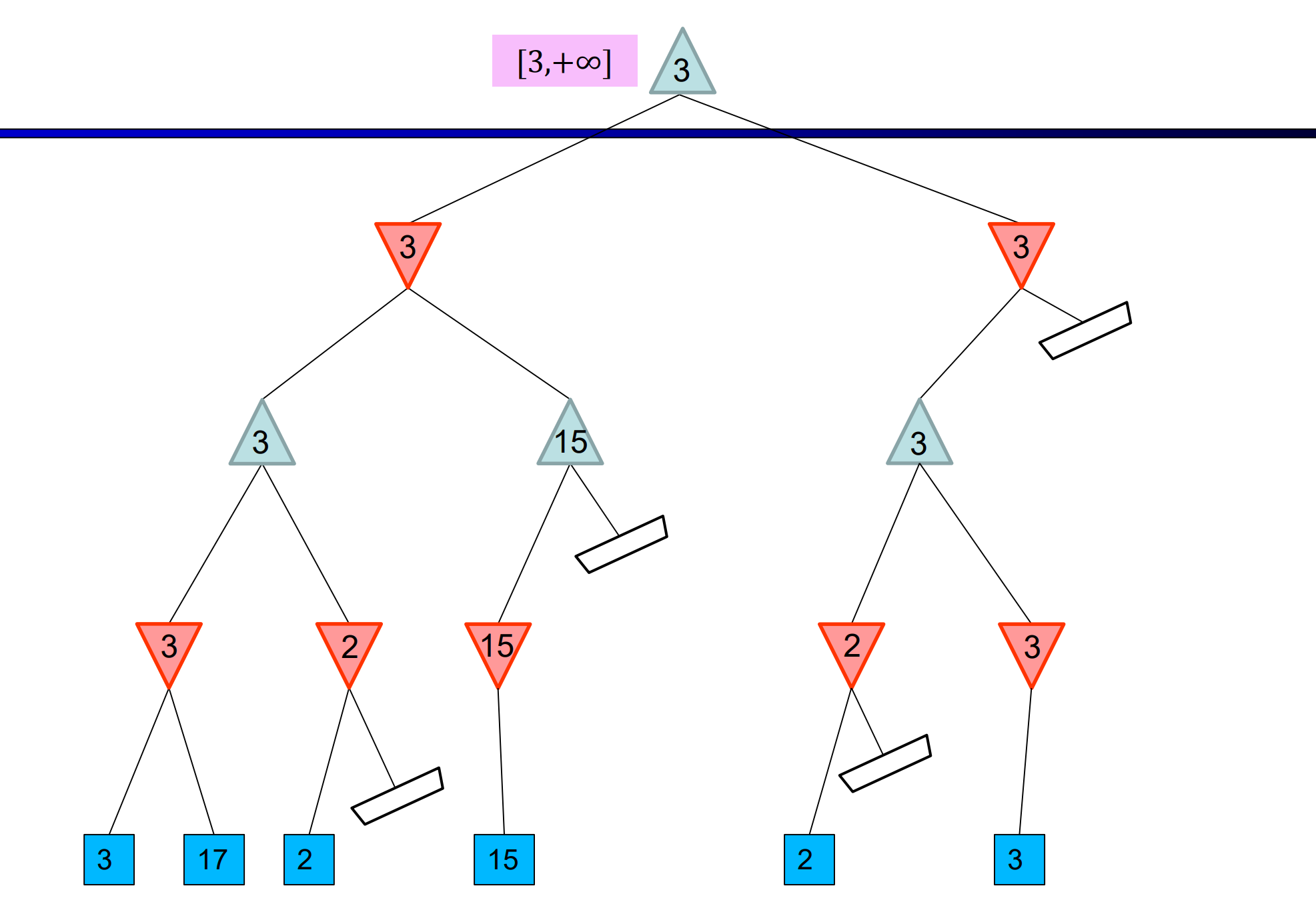
  • alfa-béta nyesés

    • ötlet: feleslegesen kiértékelt ágak lenyesése, a játékosok ezeket biztosan nem választják, valamint gyerek csomóópontok sorrendezése ami növeli a hatékonyságot
    • éppen az n csomópont MIN-ÉRTÉKét számítjuk ki, végig lépkedünk n gyerekein
    • n gyerekeinek minimum értéke egyre csökken(het), mert MIN erre törekszik
    • legyen m és m' két másik már megvizsgált csomópont, amelyeket MAX választhat
    • ha n rosszabbá válik mint m vagy m', akkor MAX el fogja kerülni n-t, így nem kell megvizsgálni n további gyerekeit
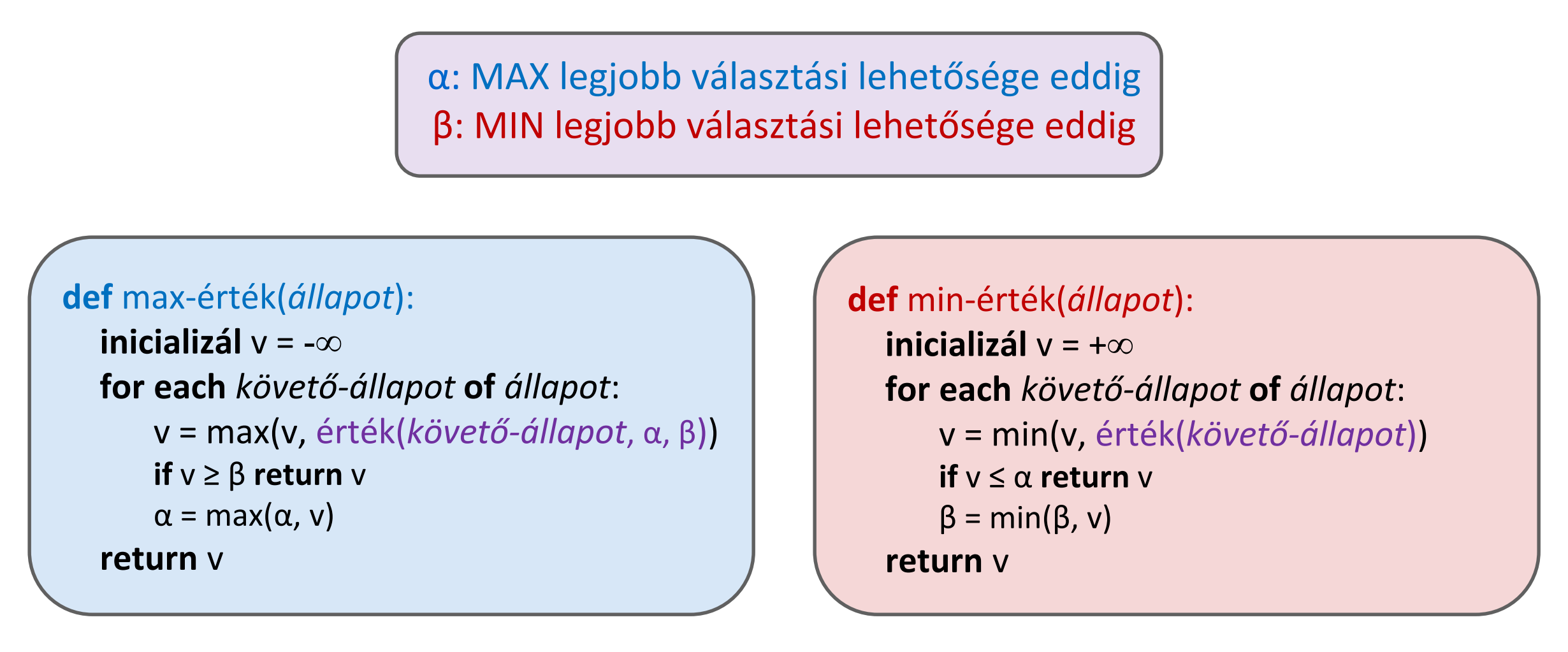
    • algoritmus: image-20201022171942176
    • hatás:
      • nyesés nem befolyásolja a gyökér csomópont minmax értékét!
      • köztes csomópontok értéke eltérhet a valóságtól
      • gyerek csomópontok jó sorrendezése növeli a nyesés hatékonyságát
      • tökéletes sorrendezéssel:
        • idő: O(bm)-ről O(bm/2), mert az elágazási tényező b = gyök b-re csökkent
        • így dupla keresési mélység valósítható meg!
    • példa:
    • image-20201022180230909

Erőforrások limitációja

  • probléma: keresés nem tud eljutni a levélcsomópontokig!
  • megoldás: mélységkorlátozott keresés
    • végállapotok hasznossága helyett egy kiértékelő függvény általi becslést fogunk adni
  • probléma: optimális játék nem garantált
  • ha bármikor le kell tudni állni → iteratívan mélyülő keresés kell
  • kiértékelő függvény
    • sakknál → jegyek súlyozott lineáris kombinációja f1(s) = (világos vezérek száma - sötét vezérek száma)
      • ha sok értékes bábunk van még, az többet ér!
    • kiértékelő függvények mindig pontatlanok
    • számít, hogy milyen mélységben vagyunk → a sakk játék vége fele már érdemes kiszámítani az optimális lépést!

Bizonytalan kimenetelek

Legrosszabb eset vs átlagos eset

  • ötlet: bizonytalan kimeneteleket a véletlen irányítja, nem egy ellenfél

Expectimax keresés

  • explicit véletlen → kockadobás
  • véletlenszerűen viselkedő ellenfelek → PacMan szellemek véletlen mozgása
  • cselekvés nem sikerül → robot mozgásánál megcsúszik a kerék
  • fontos: az értékeknek az átlagos kimenetelt kellene tükrözniük (expectimax), nem pedig a lehető legrosszabb (minimax) kimenetelt
  • expectimax keresés
    • ötlet: számítsuk ki az átlagos pontszámot (hasznosságot) optimális játékot feltételezve
    • max csomópontok → mint minmax keresésnél
    • min csomópontok → véletlenszerűek, bizonytalan a kimenetel
    • kérdés: várható érték = gyerekcsomópontok súlyozott átlaga
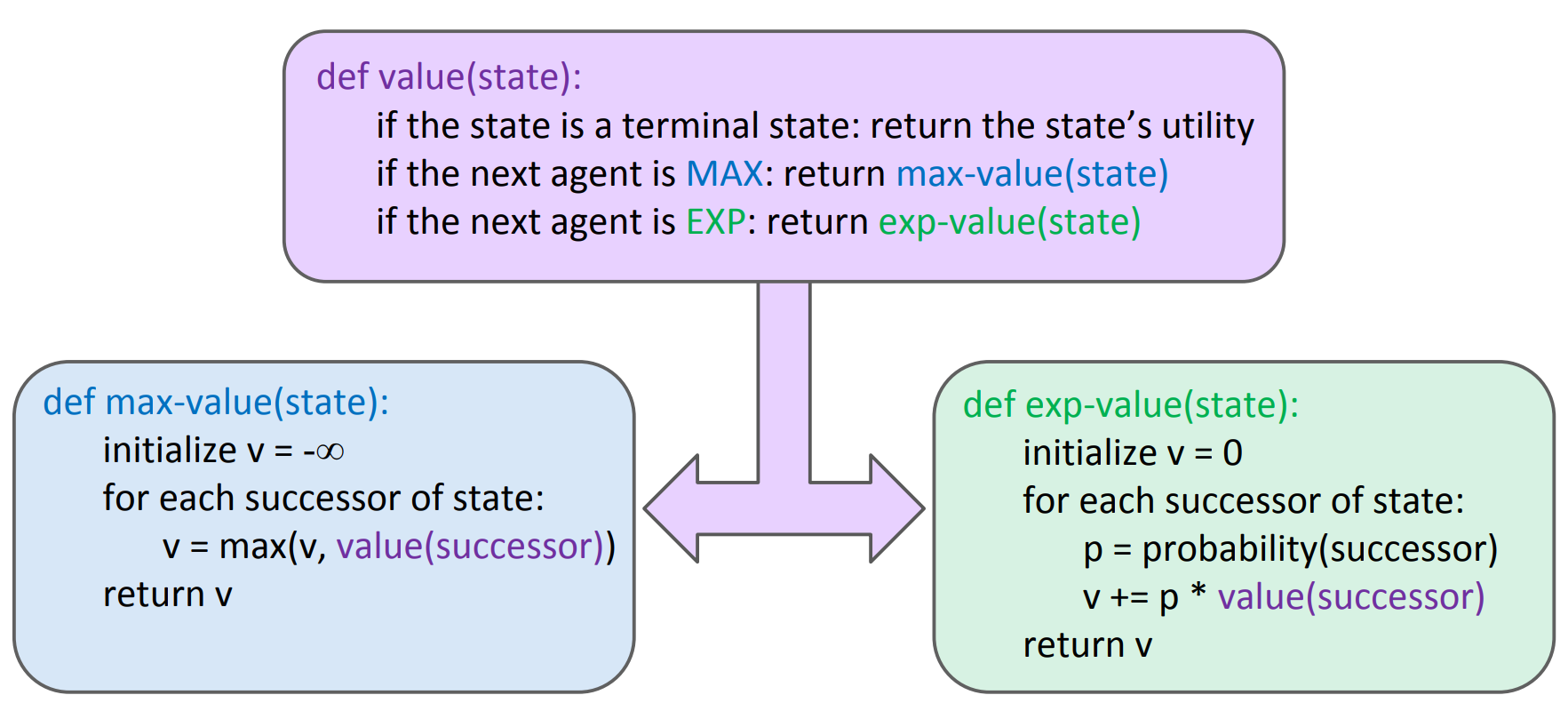
    • algoritmus: image-20201022183811669
    • hasznosságot súlyozzuk a bekövetkezésük valószínűségével!
  • itt is lehet nyesni

valószínűségek

  • véletlen változó → eseményt reprezentél, melynek kimenetele nem ismert
  • valószínűségi eloszlás → súlyok hozzárendelése kimenetelekhez
  • valószínűségi axiómák: valószínűségek nem negatívak, összes lehetséges kimenetel valószínűségeinek összege 1
  • keresésnél használt valószínűség kiszámítása
    • lehet egyszerű egyenletes eloszlás, vagy bonyolultabb nagy számítási igényű számolás
    • fontos a modellezésnél: ne legyen se túl pesszimista, se túl optimista!
támadó szellem random szellem
minmax pacman erre lett kitalálva ezt is jól kezeli
expectimax pacman :( ez nagyon nem jó ez is jól kezeli, és jobban is teljesít itt a minmax-nál

Kevert rétegű játék

  • expectiminimax
    • környezet egy plusz véletlen ágens, aki a minmax játékos után lép
  • ismételt véletlen mintavétel, ezen minták gyakorisága alapján közelítjük a nehezen számítható értékeket
  • MCTS
    • Kiválasztás → fa mely részét bontsuk ki tovább (már exploration - már feltárttal foglalkozunk, exploitation- újat tárunk fel)
    • Terjeszkedés → következő csomópont kiválasztása (már bevált ág folytatása VAGY további lehetséges lépés felfedezése)
    • Szimuláció → véletlenszerű módon leszimuláljuk a játék további részét
    • Visszaterjesztés → ennek eredményét beírjuk a fába
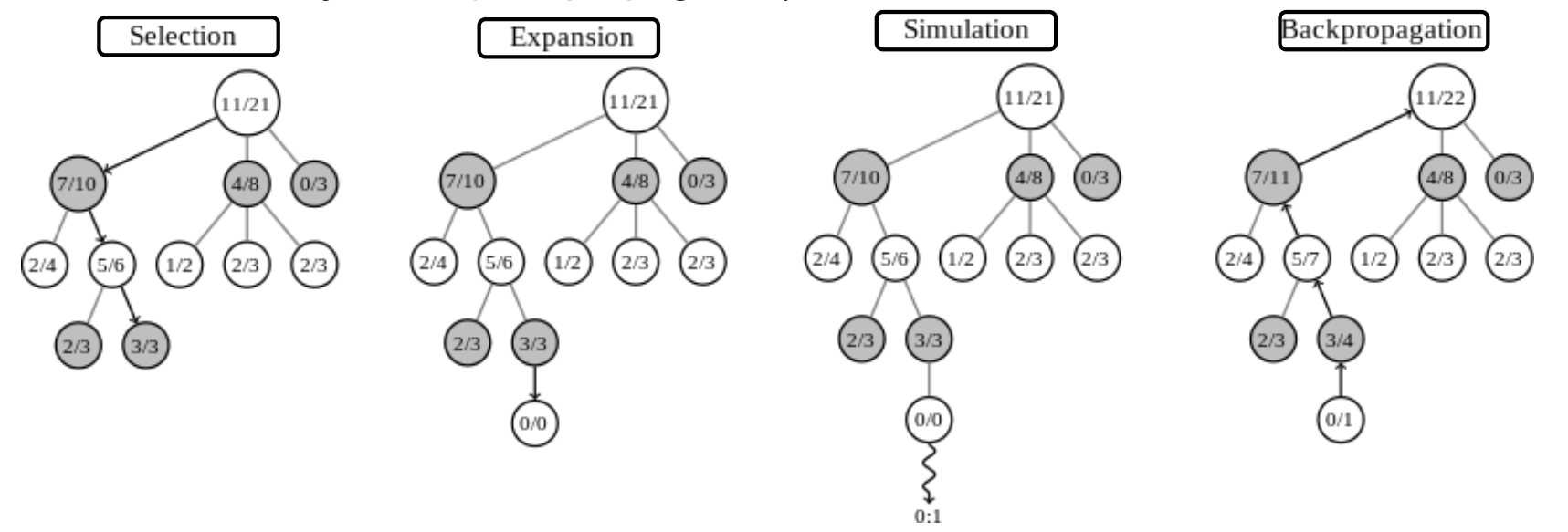
    • image-20201022190022649
    • fontos: kihasználás és feltárás közti arány → azt kell jól csinálni!
    • image-20201022190211682