Mesterséges intelligencia - 2. előadás
Problémamegoldás kereséssel

Letöltés PDF-ként

Ismétlés

Ágens

• szenzorokon keresztül érzékeli a környezetet
• beavatkozó szerveken keresztül cselekszik, azaz befolyásolja a környezetét

Racionális ágens

• úgy választ a lehetséges cselekvések közül, hogy általuk maximalizálja a várható hasznosságot
  • egyszerű eset → rendelkezik céllal, ismeri a költségeket
  • komplex eset → hasznossági függvénnyel rendelkezik, várható jutalmakat ismeri (cél a jutalom maximalizálása)

Környezet

• fontos figyelembe venni az ágens tervezésének szempontjából
• teljesen / részlegesen megfigyelhető → memória kell a belső állapot nyilvántartására
• diszkrét / folytonos → folytonosnál nem lehet az összes állapotot megkülönböztetni
• sztochasztikus / determinisztikus → több lehetséges forgatókönyvvel is kell dolgozni sztochasztikus esetben
• egyedüli ágens / több ágens → lehet, hogy véletlenszerűen kell viselkednie

Reflex ágens

• aktuális érzékelés vagy memória alapján választ cselekvést
• környezetet nyilvántarthatja memóriában (belső modell a világról)
• nem veszi figyelembe a cselekvések jövőbeli következményeit

Tervkészítő ágens

• döntéshozatalnál a lehetséges következményekkel is számol
• belső modell a világról (hogy hogyan változik a cselekvése hatására)
• kell neki egy cél, ami tesztelhető célfüggvénnyel

Keresési problémák

• keresési probléma elemei:
  1. állapottér
  2. állapotátmenet-függvény, formája: (cselekvése, költségek)
  3. kiindulási állapot
  4. célállapot teszt
• megoldás → cselekvések egy sorozata (terv), kiindulási állapotból célállapotba juttat
• Példa - Útvonaltervezés
  1. állapottér →  városok
  2. állapotátmenet-függvény → utak, költség a távolság
  3. kiindulási állapot → pl Arad
  4. célállapot tesztelés → állapot == Bukarest?
• állapottér nagysága → könnyen túl nagy lehet
  • elég csak a nagy valószínűséggel bekövetkező lehetőségeket számba venni

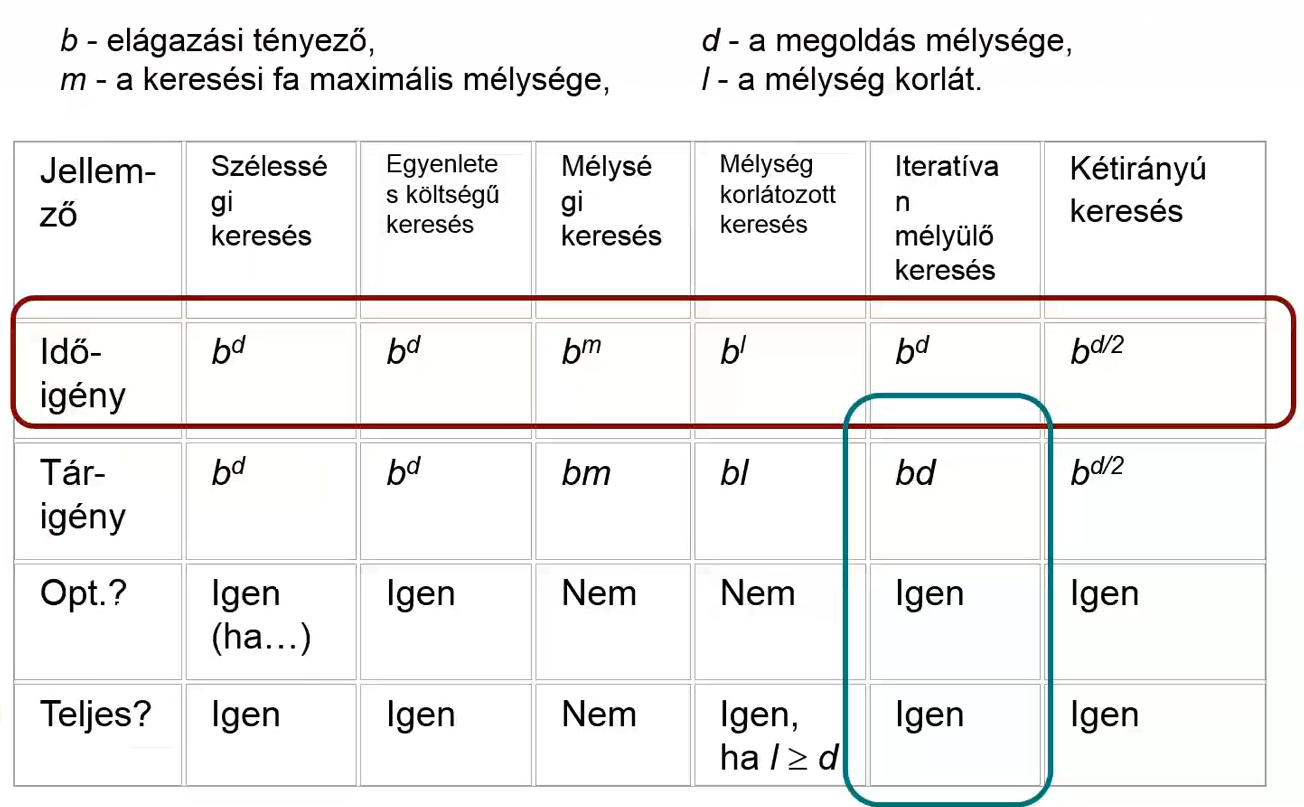
Keresési eljárás tulajdonságai

• Teljesség (completeness) → ha van megoldás, biztosan megtalálja
• Időigény (time complexity) → mennyi idő a megoldás megtalálása
• Tárigény (space complexity) → mennyi tárhely kell
• Optimalitás (optimality) → ha több megoldás van, megtaláltuk e a legjobbat?

Állapottér reprezentáció

Állapottérgráf

• csomópontok a világ állapotának egy egy absztrakt reprezentációi
• élek → állapot átmenetek
• célteszt → célállapot elérésének vizsgálata
• minden állapot 1x fordulhat elő
• probléma: nagyon nagy lesz, teljes egészében nem lesz felépíthető a memóriában

Keresési fa

• start: gyökér csomópont
• levelek: lehetséges jövők
• csomópontok → olyan állapot, amit tartalmaz egy adott terv
• probléma: teljes egészében nem lesz felépíthető a memóriában

Állapottérgráf vs keresési fa

• keresési fa 1 csomópontja = egy útvonal az állapottérgráfban
• kört tartalmazó állapottérgráfhoz → végtelen fa kellene!

Keresés keresési fával (általánosan)

• perem = potenciális terv folytatások
• 
• a különböző algoritmusok a stratégiában fognak különbözni, amivel a következő vizsgált perem pont lesz kijelölve

Keresési stratégiák

• nem informált keresések (gyenge, vak keresés)
  • tudjuk: hogyan néz ki a célállapot
  • nem tudjuk: merre a cél, milyen költségű oda a legrövidebb út
• informált keresések (heurisztikus keresések)
  • tudjuk: hogyan néz ki a célállapot
  • jó becslésünk van rá: merre lehet a célállapot, milyen költségű a célállapotba vezető út

Mélységi keresés (DFS)

• stratégia: legmélyebb csomópont kifejtése (legbaloldalibb ág a fában)
• megvalósítás: a perem egy LIFO stack
• legrosszabb eset → teljes fa feldolgozása
• elágazási faktor = b (egy szinten hány gyerek van)
• maximum mélység = m
• jellemzése:
  1. Teljesség → bal oldallel kezd, teljes fát is feldolgozhatja
     • feltétel: m legyen véges → O(b^m) időt vesz igénybe
  2. Időkomplexitás
  3. Tárkomplexitás → csak a gyökércsomóponthoz vezető úton levő elágazások számítanak → O(bm) :)
  4. Optimalitás → nem, legbaloldalibb megoldást találja meg, költségtől és mélységtől függetlenül :(
• baj: ha jobb oldalt van a megoldás

Szélességi keresés (BFS)

• strarégia: a legkevésbé mélyen levő csomópont kifejtése (szintenként)
• megvalósítás: a perem egy FIFO sor
• jelenlegi mélység = s
• jellemzése:
  1. Teljesség → legfelső szinttel kezd, teljes fát is feldolgozhatja (s véges, ha létezik megoldás)
     • feltétel: O(b^s) időt vesz igénybe
  2. Időkomplexitás
  3. Tárkomplexitás → kb a legutolsó szinttel arányos: O(b^s) :(
  4. Optimalitás → igen, ha minden egységesen 1 költségű :)
• baj: ha mélyen van a megoldás

Mélységkorlátozott keresés

• utak maximális mélységére (m) vágási korlátot ad
  • ha ezt eléri a keresés, akkor visszalép
• Teljesség → ha a vágás felett van a megoldás (ha nem, akkor gáz van)
• Optimalitás → nem optimális (nem garantálja a legkisebb költségű utat)
• baj: honnan tudjuk a korlátot?

Iteratívan mélyülő keresés

• ötlet: jó ez a mélységkorlátozós dolog, de nehéz belőni a jó korlátot
• megoldás: kipróbáljuk az összes lehetséges mélységkorlátot
• baj: redundáns lesz, olyat kell feldolgozni amit már egyszer feldolgoztunk
• Optimális és teljes → mint a szélességi keresésé
• Tárhelykomplexitása alacsony → mint a mélységi keresésé
• kifejtések száma, ha d mélységben b elágazási tényező mellett
  • szélességi keresésnél → 1 + b + b² + ... + b^d-2 + b^d-1 + b^d
  • iteratívan mélyülő keresésnél → (d+1)*1 + (d)*b + (d-1)b² + ... 3b^d-2 + 2b^d-1 + 1b^d
    • mivel a fa felsőbb részeit többször kifejti
  • minél nagyobb az elágazási tényező, annál kisebb lesz a többletmunka

Költségérzékeny keresés

Egyenletes költségű keresés (UCS)

• stratégia: legkisebb költségű csomópont kifejtése
• módszer: perem egy prioritásos sor lesz, ahol a prioritás a kumulált költségnek felel meg
• 
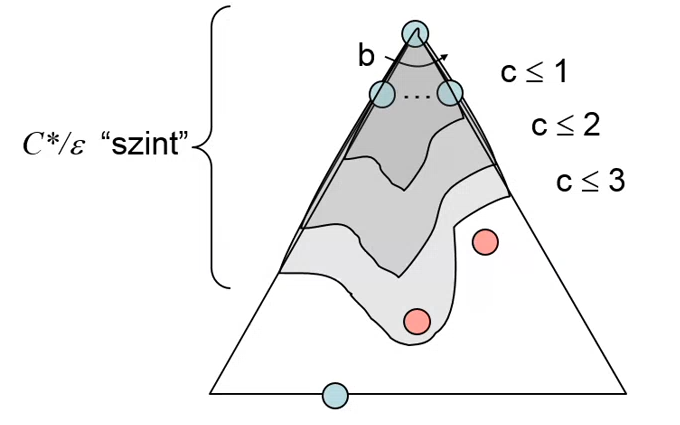
• elv: kifejti az összes olyan csomópontot, ami kevesebb költséggel elérhető, mint a legkisebb költségű megoldás
• C* = megoldás költsége, ε = élek legalább ε költségűek (minimum élköltség)
• effektív mélység = C*/ε
• Teljesség → igen, ha a legjobb megoldás véges költségű és a minimum élköltség pozitív!
• Optimális → IGEN :)
• Tárhelykomplexitás → kb az utolsó szinttel arányos O(b^C*/ε)
• Időkomplexitás → O(b^C*/ε)
• baj: minden irányba feltár, fogalma sincs a célállapot helyzetéről

Eddigi algoritmusok közös tulajdonságia

• Csak a perem tárolásának módjában különböznek
  • mind valamilyen prioritásos sort használnak
• mélységi → verem
• szélességi → sor

Kétirányú keresés

• egyszerre indítunk keresést előre a kiinduló állapotból és hátra a célállapotból
• keresés véget ér, ha találkozik a két keresés
  • O(2 * b^d/2) = O(b^d/2)
• implementálása nem triviális
  • hogy keresünk hátrafele? → több célállapot esetén nehéz

Eddigi keresések összefoglalója

Informált keresés

Heurisztika, h(n)

• ötlet: büntessük, ha a céltól távolodunk = jutalmazzuk, ha közeledünk
• egy függvény, ami becslést ad arra, hogy az adott állapot mennyire van közel a célállapothoz
• mindig az adott keresési problémához tervezett (pl: Manhattan távolság, euklidészi távolság)
• minden n állapotra ki kell számítani
• ha teljesen pontos lenne, akkor felesleges (egyértelmű a megoldás)
• teljes útköltség = eddig megtett út költsége + hátralevő út költsége → f(n) = g(n) + h(n)

Mohó keresés

• stratégia: fejtsük ki azt a csomópontot, amiről azt gondoljuk, hogy a legközelebb van a célállapothoz
  • heurisztika: a legközelebbi célállapottól való becsült távolság
• probléma: nem biztos, hogy az aktuálisan legjobb állapot lesz a legjobb globálisan
• legrosszabb esetben egy rosszul irányított mélységi keresést kapunk
• Teljesség → nem teljes (elindul végtelen úton, nem tér vissza mást kipróbálni)
• Optimális → nem optimális
• Idő és Tárigény → nagyon rossz, az összes csomópontot a memóriában tartja → O(b^m)

A* keresés

• ötlet: egyenletes költségű és mohó keresést kombináljuk
  • egyenletes költségű → g(n) minimalizálása a célja
  • mohó → h(n) minimalizálása a célja
  • 
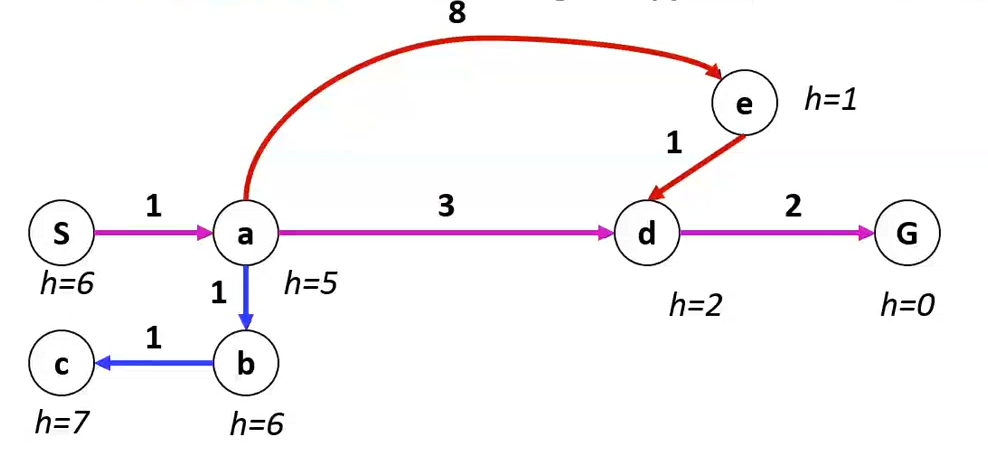
• vegyük figyelembe az eddig megtett út költségét és a hátralevő út költségét is → f(n) = g(n) + h(n)
• csak akkor állhatunk meg, ha már kifejtésre került a célállapot (nem elég, ha a kifejtendők közt van, mert az utolsó út is számít)
• Teljes és Optimális → igen, ha jó a heurisztika
• A határvonala a cél fele van (az egyenletes költségűé egyenletes minden irányba)

Elfogadható heurisztika

• nem elfogadható (pesszimista) heurisztika megtöri az optimalitást azzal, hogy jó tervek a peremben maradnak
• elfogadható (optimista) heurisztika "lelassítja" a rossz terveket, de sosem lép túl a valós költségeken
  • 0 ≤ h(n) ≤ h*(n), ahol h*(n) a valós költség a legközelebbi célállapothoz
• A* kereséshez elengedhetetlen az elfogadható heurisztika kialakítása!
• heurisztika készítése → probléma relaxálásával (egyszerűsítésével) → pl légvonal, manhattan távolság stb