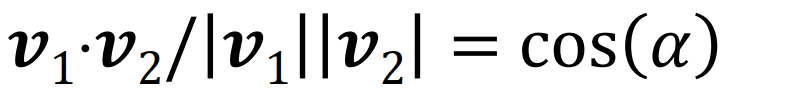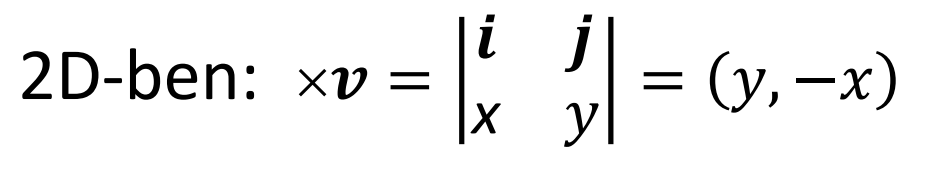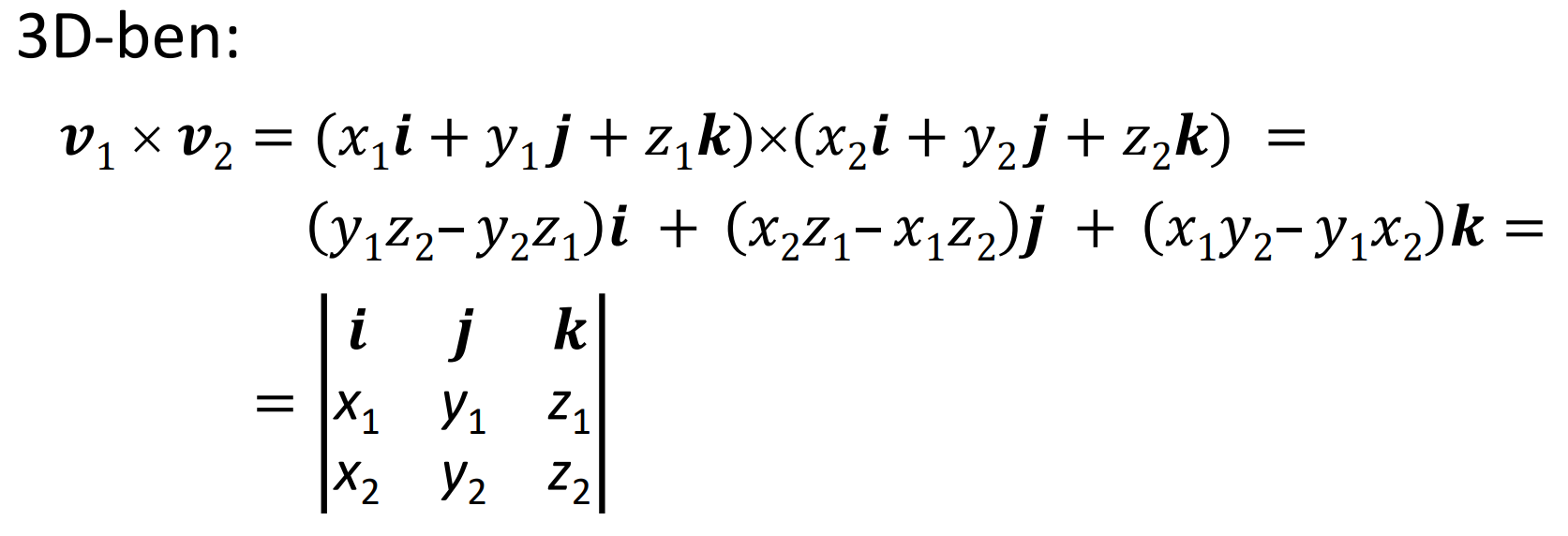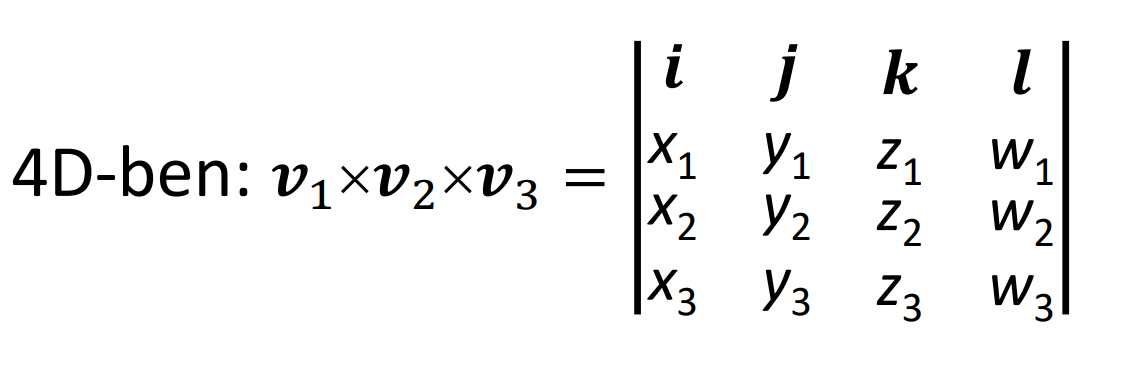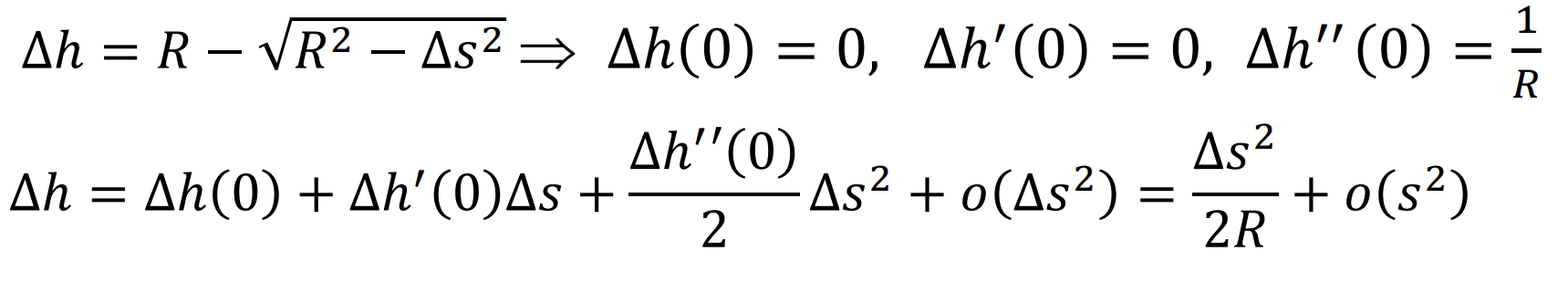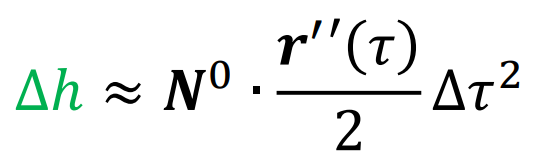Kikérdező
1. előadás¶
Klasszikus geometriák¶
Sorold fel a tanult klasszikus geometriákat, és hasonlítsd össze őket!
- 4 tanult geometria van
-
Euklidészi síkgeometria
- Egy egyeneshez egy rajta kívül fekvő ponton át egy nem metsző egyenes húzható → párhuzamosság
- háromszög szögösszege 180 fok
- pithagorasz tétel → a2 + b2 = c2
- kör területe → πR2
-
Gömbi geometria
- állandó pozitív görbületű (bármely irányba körbenézve olyan, mintha egy dombtetőn állnánk)
- két egyenes mindig metszi egymást egy pontban → átmérő
- egyenes = főkör = legrövidebb út
- az egyenesek mindig metszők
- háromszög szögösszege több mint 180 fok
- pithagorasz tétel → a2 + b2 > c2
- kör területe → több mint πR2
-
Hiperbolikus geometria
- állandó negatív görbületű (vannak olyan irányok, ahonnan nézve a domb tetején vagyunk, és van, ahonnan a völgyben)
- Egy egyeneshez egy rajta kívül fekvő ponton át több nem metsző egyenes húzható → több párhuzamos van
- egyenes = legrövidebb út
- háromszög szögösszege kevesebb mint 180 fok
- pithagorasz tétel → a2 + b2 < c2
- kör területe → kevesebb mint πR2
-
Projektív geometria
- lényeg: a "végtelen" is része a síknak!
- Két egyenes pontosan egy pontban metszi egymást → a végtelenben = ideális pontban
- nincsenek párhuzamosok (mert mindenegyik egyenes mindegyiket metszi)
- programozási előny → nincs szingularitás és speciális eset, mivel nincsenek párhuzamosok
-
Mi az a Mercantor térkép?
- olyan térkép, ami szögtertó, de torzítja a távolságot és a területet
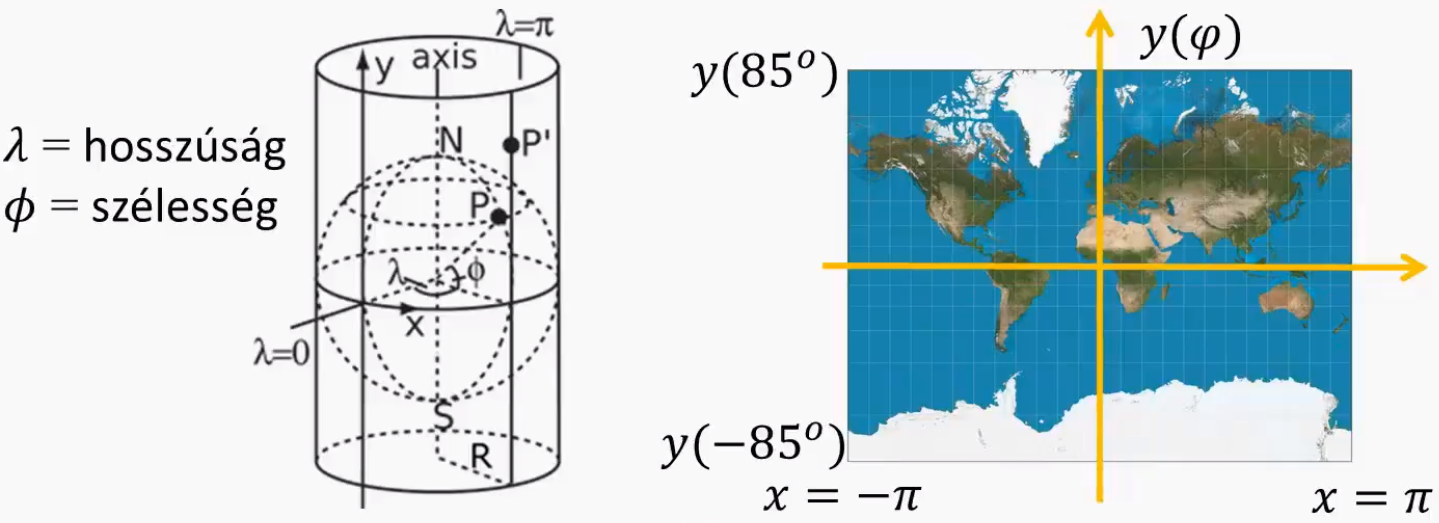
- A gömböt befoglaljuk egy hengerbe, majd annak egy pontját rávetítjük a henger falára, és a hengert (mivel 0 görbületű), már ki lehet teríteni torzulás nélkül a síkba. Ezen kívül függőlegesen torzítjuk, hogy a szögek megfeleljenek.
- torzítás: x = λ és y = log(tan( π/4 + φ/2))
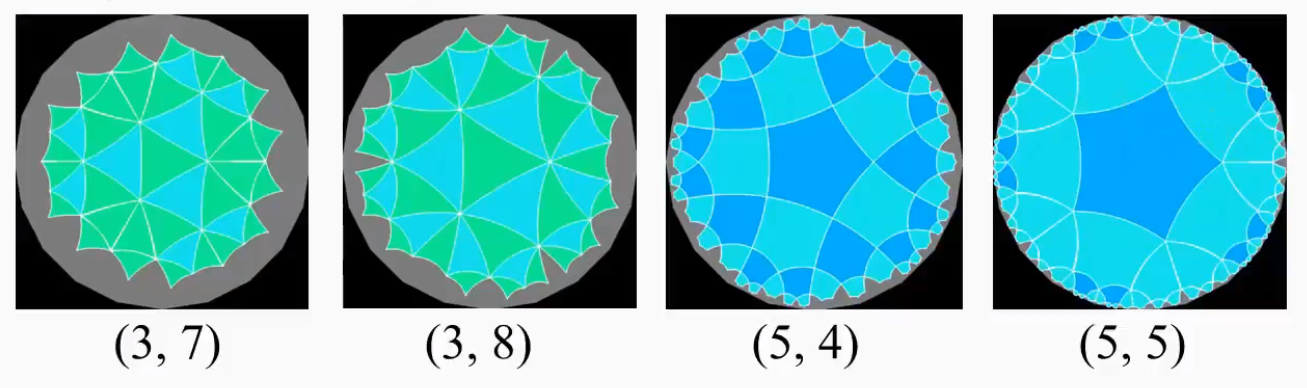
Szedd össze a tesszellációról tanultakat!
- a tesszelláció jelentése: szabályos, egybevágó sokszögekkel való csempézés
- Euklidészei geometria esetén csak (3, 6), (4, 4) és (6, 3) csempézés létezik
- Hiperbolikus geometria esetén végtelen sok, mivel a sokszögek belső szöge bármilyen értéket felvehet
Hasonlítsd össze a tanult klasszikus geometriákat a metsző egyenesek és a görbületük szempontjából!
| Euklideszi | Gömbi | Hiperbolikus | Projektív |
|---|---|---|---|
| 1 nem metsző egyenes (párhuzamos) | 0 nem metsző egyenes | egynél több nem metsző egyenes | 0 nem metsző egyenes |
| zérus görbületű | pozitív görbületű | negatív görbületű | nem metrikus: végtelen is része |
Vektoralgebra¶
Mi a vektor?
- a vektor
- írány és távolság
- eltolás
- két pont viszonyát jellemzi
Mutasd be a pontok és valós számok közötti tanult kapcsolatokat!
- mérések → pontok és vektorok számszerűsítése (PONTOK → VALÓS SZÁMOK)
- távolság rendelése pontpárhoz, hossz rendelése a vektorhoz és szög rendelése két vektorhoz
- pontok megadása függvénnyel (VALÓS SZÁMOK → PONTOK)
- r(t), ahol t például az idő paraméter → egy görbe
- pontok leképzése valós számokká → pl minden térpontban megmérjük a hőt
- transzformációk → (PONT → PONT)
Sorold fel a tanult vektorműveleteket!
-
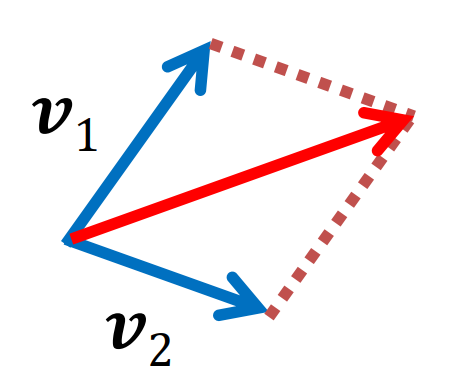
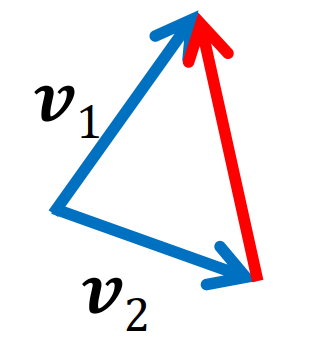
összeadás és kivonás
- összeadás → v = v1 + v2
- kivonás → v = v1 - v2
- kommutatív és asszociatív
- összeadás → v = v1 + v2
-
skálázás
- skalárral való szorzás → v1 = α*v
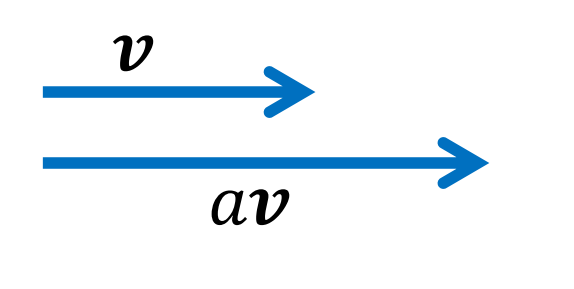
- disztributív
-
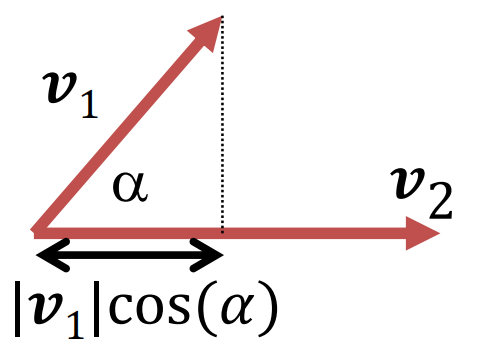
skalár szorzat (dot)
- v1 * v2 = |v1|*|v2|*cos(α)
- jelentése: egyik vektor vetülete a másikra * másik hossza
- tulajdonságok: nem asszociatív, de kommutatív és disztributív az összeadásra
- vektor hosszának kiszámítása → saját magával vett skaláris szorzata → v * v = |v|2
- egységbektor képzése → vektor elosztva az abszolútértékével
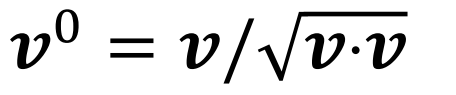
- (vektor elosztva a saját magával vett skaláris szorzatának négyzetgyökével)
- 2 vektor bezárt szögének koszinusza
- két vektor merőleges, ha skalár szorzatuk nulla
-
vektor szorzat (cross)
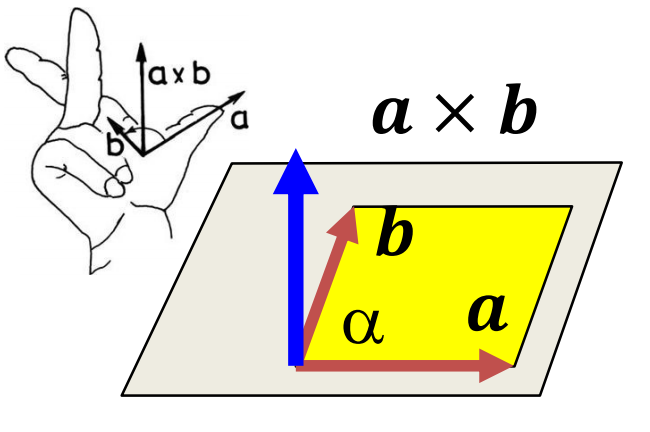
- |v1 × v2| = |v1|*|v2|*sin(α) → merőleges a két operandus által meghatározott síkra, majd ebből a jobbkézszabály szerinti
- jelentése:
- operandusok által kijelölt terület
- operandusokra merőleges vektor
- (egyik vektor vetülete a másikra merőleges síkra + 90°-os elforgatás) * másik hossza
- tulajdonságok: nem asszociatív, antiszimmetrikus (a × b = −b × a), disztributív az összeadásra
- |v1 × v2| = |v1|*|v2|*sin(α) → merőleges a két operandus által meghatározott síkra, majd ebből a jobbkézszabály szerinti
Mi az iránymenti derivált, és a gradiens
- kiindulás: geometriánk minden pontjához egy skalár értéket rendelünk (pl pontban levő hőmérséklet), azonos hőmérsékletű pontokból szintvonalak lesznek
- iránymenti derivált:
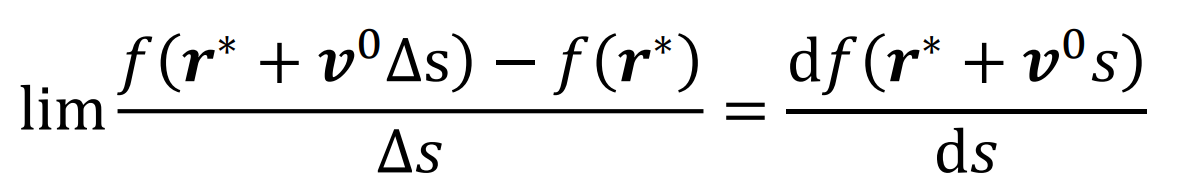
- (egy v0 irányba Δs-el arrébb menve)
- gradiens: amerre ez az iránymenti derivált maximális →
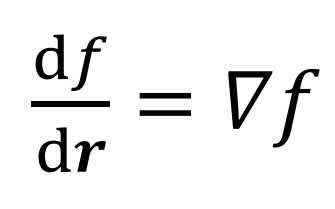
- (a szintvonalra merőleges irányba lesz a gradiens)
Mutasd be a paraméter szerinti deriválást
- ide kellene még valami?
Mutasd be a kontravariáns és a kovariáns kordinátarendszerek közti különbségeket!
- koordinátarendszer = geometriai referencia rendszer + hozzá tartozó mérési utasítás
-
Kontravariáns koordinátarendszer
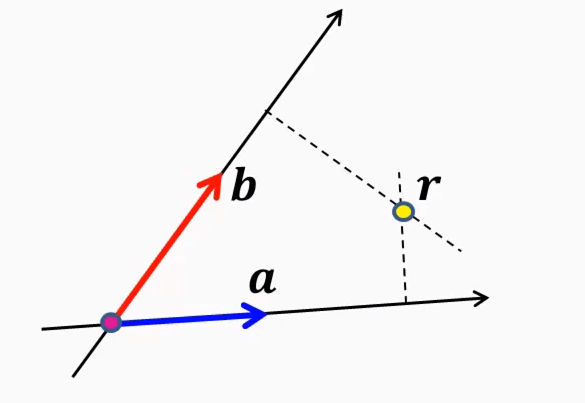
- az a és b vektort hányszor kell venni, hogy eljussunk az r pontba → r(x, y) = x***a* + y***b*
- a = r'x és b = r'y
- kontravariáns = ha megdublázzuk a bázisvektorokat (a, b), és szintén r-t akarjuk kifejezni, akkor a koordinátákat feleznünk kell (x, y)
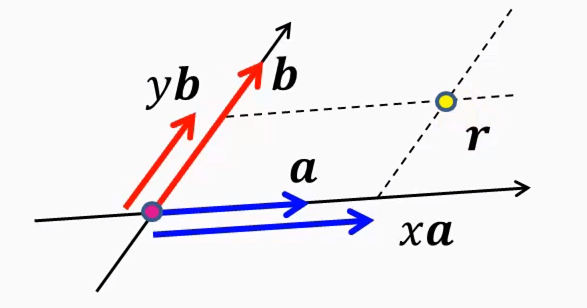
- az a és b vektort hányszor kell venni, hogy eljussunk az r pontba → r(x, y) = x***a* + y***b*
-
Kovariáns koordinátarendszer
- vetítjük a pontot az egyenesekre
- paraméter vonalak merőlegesek a koordináta tengelyekre (az adott koordináta tengelyre merőleges egyenesen lesznek az azonos koordinátájú pontok)
- X = a * r és Y = b q* r
- a = ∇X, b = ∇Y
- kovariáns = egy irányba változik X és Y a bázisvektorokkal
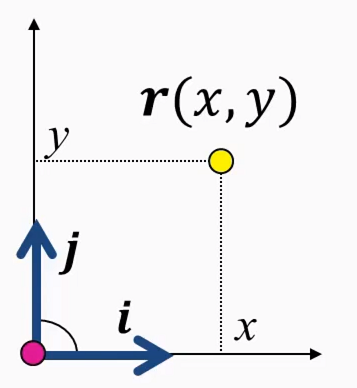
Mutasd be a Descartes koordináta rendszert!
- alaptulajdonsága: bázisvektorai egység hosszúak és egymásra merőlegesek → a kontravariáns és kovariáns koordináták megegyeznek
- r(x, y) = x***i* + y***j*
- x = i * r és y = j * r
- r'x = i és r'y = j
- i = ∇x és j = ∇y
-
műveletek Descartes koordinátákkal:
-
vektoriális szorzat 2-3-4D-ben
Differenciálgeometria¶
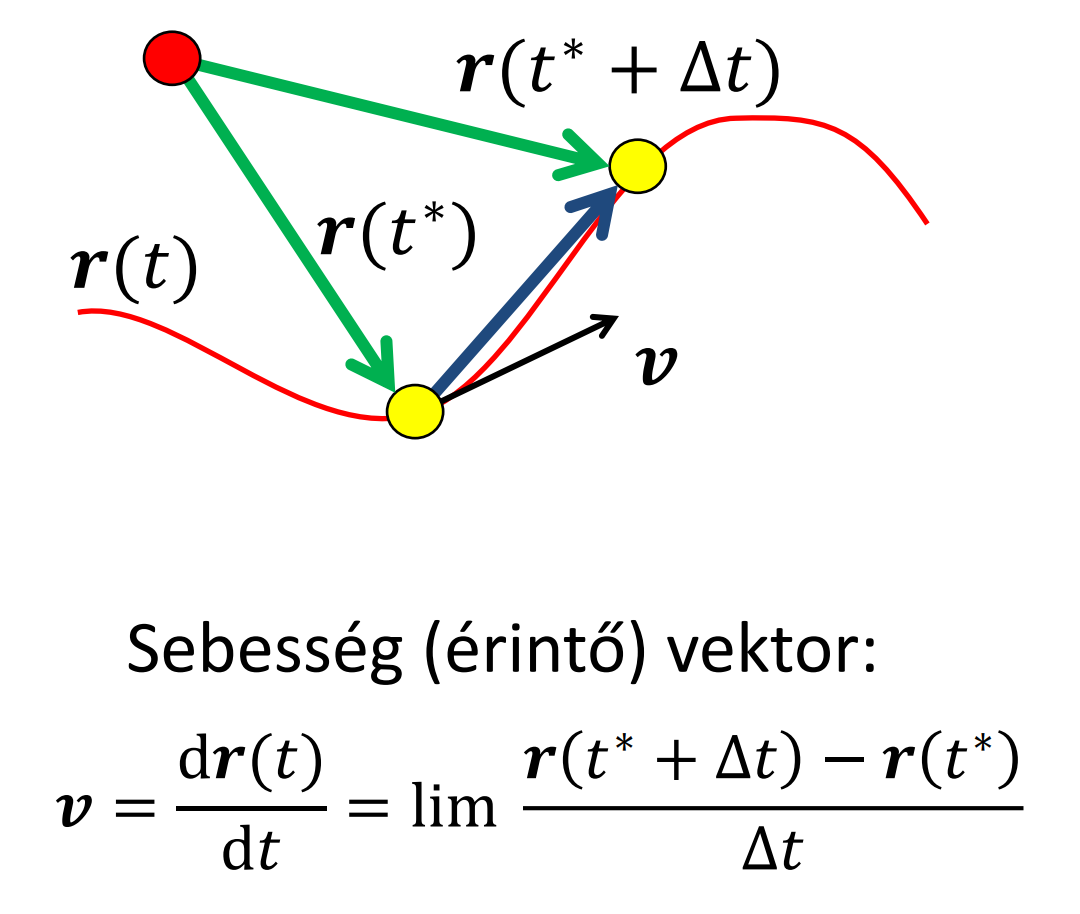
Mutasd be egy síkgörbe érintőjét és normálvektorát!
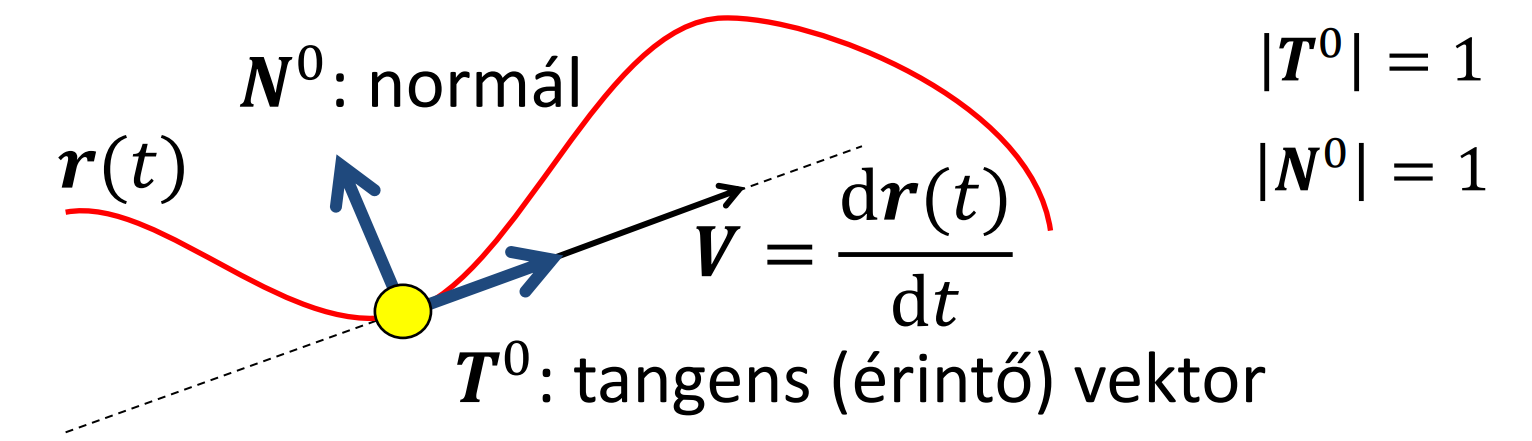
- görbe = mozgás → mivel a dinamika nem érdekes, a t nem feltétlenül idő
- érintő iránya (v) → sebességvektor, ami a pálya idő szerinti első deriváltja
- normálvektor → érintőre merőleges → (Nx, Ny) = (-Ty, Tx)
- gyorsulás → a pálya idő szerinti második deriváltja
- érintő irányú komponens (tangenciális) → pályamenti sebességet gyorsítja vagy lassítja
- normál vektor irnyú komponens → sebesség irányát módosítja
- sebesség állandó = érintő irányú gyorsulás nincsen (csak centripetális, ami a pontot a görbülő pályán tartja)
Mi a görbület?
- görbület jele: κ
-
4 definíciót tanultuk a görbülethez:
- egysebességű mozgás centripetális gyorsulása → acp = v2/ R
- az a gyorsulás, amit el kell szenvednünk, ha végigautózunk ezen a görbén, mégpedig állandó egységsebességgel
- másodrendben simulókör sugarának reciproka →
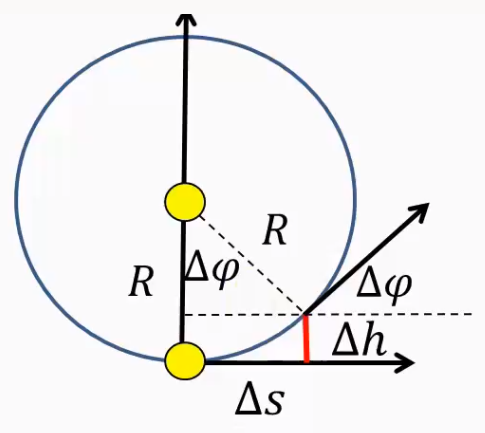
- érintő elfordulása kis lépésnél → Δφ ≈ sin(Δφ) = Δs / R
- az az eltávolodás, ami Δs kicsiny távolság megtételekor megfigyelhető
- ezekből adódóan →
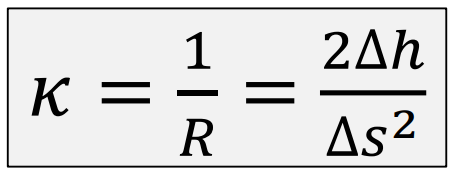
- egysebességű mozgás centripetális gyorsulása → acp = v2/ R
Hogy számíthatunk görbületet?
- a következő képletet fogjuk használni:
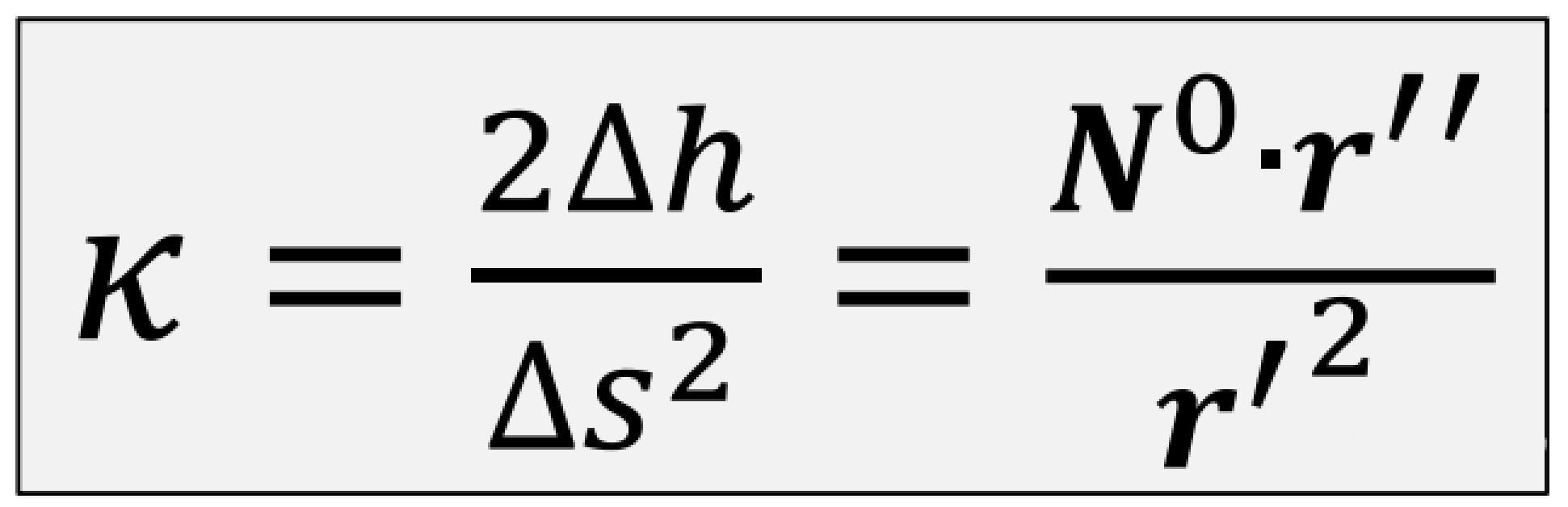
- ahol r'2 az első fundamentális forma, r'' pedig a második fundamentális forma
- kezdjük a Δs2 (lépéshossz négyzete) kiszámolásával
- másnével metrika → ha a koordinátát egy picikét megváltoztatjuk, akkor ténylegesen a térben mekkora távolságot teszünk meg
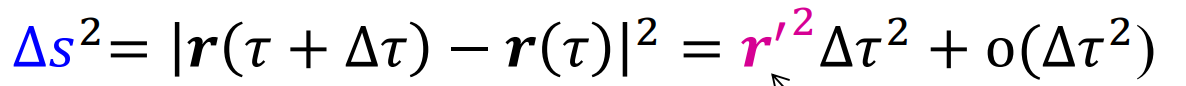
- az itt megjelenő r'2 = metrikus tenzor (1. fundamentális forma) = görbéknél, a paraméter változás négyzete és a megtett út négyzete közötti kapcsolatot a görbe deriváltjának négyzete (=sebesség négyzete) teremti meg
- majd számítsuk ki Δh-t → merőleges eltávolodás az érintőtől